多胞体
| {3,3,3} | {3,3,4} | {4,3,3} |
|---|---|---|
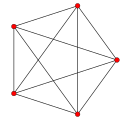 五胞体 Pentatope 4-単体 |
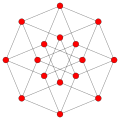
 十六胞体 Orthoplex 4-正軸体 |
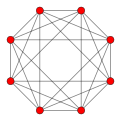
 八胞体 Tesseract 4-立方体 |
| {3,4,3} | {5,3,3} | {3,3,5} |
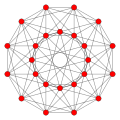 Octaplex 24胞体 |
 Dodecaplex 120胞体 |
 Tetraplex 600胞体 |
初等幾何学における四次元超多面体(4-polytope) または多胞体(たほうたい、英: polychoron, polycell, polyhedroid)は四次元の超多面体である[1][2]。四次元超多面体は連結かつ閉な図形で、より低次の超多面体図形(頂点、辺、多角形面、多面体胞)から組み立てられる。各面はちょうど二つの胞に共有される。
多くの胞からなる図形という意味で多胞体とも呼ばれるが、「多胞体」を任意の超多面体を表す polytope の訳語としても用いることがある[注釈 1]ため注意が必要である。以下、誤解の虞が無いならば、断りなく四次元超多面体の意味で多胞体と呼ぶことにする。
多胞体は二次元の多角形および三次元の多面体の四次元における対応物である。
位相的には、多胞体は一様ハニカムに近い関係を持つ。例えば、三次元空間を充填する立方体ハニカムとの関係は、三次元立方体が無限正方形平面充填に関係するのと同様である。凸多胞体を「切ったり開いたり」して三次元展開図を作ることができる。
定義
編集多胞体は四次元の閉じた図形で、頂点、辺、面、胞)から組み立てられる。胞は面の三次元版で、それ自身は一つの多面体になっている。多面体の辺がちょうど二つの面と接続されていたことと対応することとして、多胞体の各面はちょど二つの胞に接続する。任意の超多面体がそうであるように、多胞体の要素全体の成す集合を適当に分割して、それ自身多胞体を成す二つ以上の部分集合にすることはできない。その意味で多胞体は素であり、合成的なものではない。
図示法
編集| 断面図 | 展開図 | |
|---|---|---|
| 投影図 | ||
| シュレーゲル図 | 二次元直交射影 | 三次元直交射影 |
多胞体は四次元的な広がりを持つのだから三次元空間内では見ることができない。しかし、それを三次元空間内の情報から視覚的に推察するための図示方法がいくつか存在する。
- 直交射影
- 多胞体の様々な対称方向を示すために直交射影は有効に用いられる。それにより頂点–辺グラフは二次元に表示でき、また目に見える射影被覆として立体面が三次元に示される。
- 投影図
- 三次元図形を平面の紙に投影するように、四次元図形を三次元に(あるいはさらに二次元に)投影することができる。よく用いられる投影図は、三次元球面上の点から三次元空間への立体射影を用いるシュレーゲル図で、三次元空間内に描かれた辺、面、胞が真っ直ぐに接続される。
- 断面図
- 多面体を曲面による切断の断面によって調べるのと同じく、多胞体を三次元「超曲面」で切った断面から明らかにすることができる。つまり、そのような断面の列を組み立てて全体の形を理解するのである。余剰の空間次元を時間的変化で代用して、これら横断面の滑らかなアニメーションを作ることもできる。
- 展開図
- 多面体の展開図が多面体の全ての多角形面が辺で繋がれた状態で同じ平面上に描かれるように、多胞体の全ての多面体胞を同じ一つの三次元空間上に面で繋げて描くことで多胞体の展開図が得られる。
位相的特徴付け
編集与えられた多胞体の位相はそのベッチ数およびねじれ係数によって決定される[4]。
多面体を特徴付ける[5]ために用いられるオイラー標数の値は、そのままでは高次元に対して意味を持たせることはできない(任意の多胞体に対して、その基礎にある位相が何であれ、その値は零である)。このようにオイラー標数が高次元の異なる位相を区別するのに不十分であったことが、より洗練されたベッチ数の発見に繋がった[4]。
同様に、多面体の向き付け可能性の概念は、トロイダル多胞体のひねり面を特徴付けるのには不十分であったから、ねじれ係数が用いられるようになった[4]。
多胞体の種類
編集正多胞体
編集四次元における正多胞体とは、3次元空間でいう正多面体に相当する多胞体のことである。定義も正多面体と似ており概要は、
- 全ての胞が一種類の正多面体でできている。
- 一つの頂点に集まる正多面体の数が同じである(頂点は合同である)。
である。正多面体をあらわす記号であるシュレーフリ記号を四次元では、構成面の形を p、構成胞の1つの頂点に集まる面の数を q、1つの辺に集まる胞の数を rとして{p, q, r} とあらわす。
4次元の正多胞体は、6種類存在する。
| 名前と三次元投影図 | 構成胞 | 構成面 | 面 | 辺 | 頂点 | シュレーフリ記号 | 対応する正多面体 |
|---|---|---|---|---|---|---|---|
| 正五胞体 |
正四面体 | 正三角形 | 10 | 10 | 5 | {3,3,3} | 正四面体 |
| 正八胞体 (超立方体) |
正六面体 | 正方形 | 24 | 32 | 16 | {4,3,3} | 正六面体 |
| 正十六胞体 |
正四面体 | 正三角形 | 32 | 24 | 8 | {3,3,4} | 正八面体 |
| 正二十四胞体 |
正八面体 | 正三角形 | 96 | 96 | 24 | {3,4,3} | (なし) |
| 正百二十胞体 |
正十二面体 | 正五角形 | 720 | 1200 | 600 | {5,3,3} | 正十二面体 |
| 正六百胞体 |
正四面体 | 正三角形 | 1200 | 720 | 120 | {3,3,5} | 正二十面体 |
双対関係は、
- 正八胞体⇔正十六胞体
- 正百二十胞体⇔正六百胞体
で、正五胞体と正二十四胞体はそれぞれ自己双対である。
半正多胞体
編集四次元における半正多胞体とは、3次元でいう半正多面体に相当する多胞体のことである。その定義は
- 全ての胞が数種類の正多面体、または半正多面体でできている。
- 全ての頂点が合同である。
4次元の場合、半正多胞体は全部で58種類ある(正多面体、半正多面体を底胞とする超角柱を含む。ただし角柱を底胞とする超角柱などの無限系列は除く)。その中には、正多胞体の頂点や辺、面を削ったものなどがある。四次元における例外的な立体が存在として捩れ二十四胞体と大反角柱の2つがある。3次元では一般的と考えられる、捩れ操作による半正多胞体は高次元では一般的ではないのである。
星型正多胞体
編集星型正多胞体とは、3次元空間でいう星型正多面体に相当する多胞体のことである。シュレーフリ・ヘスの多胞体とも言う。4次元の星型正多胞体は、10種類存在する。
| 名前 | シュレーフリ記号 |
|---|---|
| Icosahedral 120-cell | {3,5,5/2} |
| Great 120-cell | {5,5/2,5} |
| Grand 120-cell | {5,3,5/2} |
| Small stellated 120-cell | {5/2,5,3} |
| Great grand 120-cell | {5,5/2,3} |
| Great stellated 120-cell | {5/2,3,5} |
| Grand stellated 120-cell | {5/2,5,5/2} |
| Great icosahedral 120-cell | {3,5/2,5} |
| Grand 600-cell | {3,3,5/2} |
| Great grand stellated 120-cell | {5/2,3,3} |
広く定着している日本語名は現在のところない。
3次元の星型正多面体は4種類、4次元の星型正多胞体は10種類あるが、5次元以上の空間には星型正多胞体は存在しない。
一様多胞体
編集一様多胞体とは、3次元でいう一様多面体に相当する多胞体のことである。4次元の一様多胞体は現在、1849種類が確認されている。
準正多胞体
編集準正多胞体とは、3次元でいう準正多面体に相当する多胞体のことであり、一様多胞体のうち、辺の形状が合同な立体のことである。4次元の準正多胞体は、凸なものは5種類ある。
角柱・反角柱
編集3次元図形を4次元方向に平行移動すれば、そのまま角柱の4次元版が得られる。また4次元以上に現れる図形として双角柱 (duoprism) がある。これは2種類の角柱が4次元空間で絡まりあったような形状をしており、n角柱m個とm角柱n個からなる双角柱を(n - m)角柱と呼ぶ。
双対
編集四次元多胞体の双対とは、立体の数と頂点の数、面の数と辺の数を入れ替えたものをいう。
多胞体公式
編集オイラーの多面体定理の拡張としてシュレーフリの多胞体公式が成立する[6]。
ここでVは頂点の数、Eは辺の数、Fは面の数、Cは胞の数である。右辺が0となるのは多面体定理とは異なり、2次元空間の多角形で常に
となるのと同様である。奇数次元で2となるのは、空集合と全体集合(いずれも全次元共通で1個)を考慮しないためであり、これを含めて交代和を取れば全次元共通(0次元を含む)で0となる。
関連項目
編集注
編集注釈
編集出典
編集- ^ Vialar, T. (2009). Complex and Chaotic Nonlinear Dynamics: Advances in Economics and Finance. Springer. p. 674. ISBN 978-3-540-85977-2
- ^ Capecchi, V.; Contucci, P.; Buscema, M.; D'Amore, B. (2010). Applications of Mathematics in Models, Artificial Neural Networks and Arts. Springer. p. 598. doi:10.1007/978-90-481-8581-8. ISBN 978-90-481-8580-1
- ^ 例えば Coxeter 1973, p. 127
- ^ a b c Richeson, D.; Euler's Gem: The Polyhedron Formula and the Birth of Topoplogy, Princeton, 2008.
- ^ Weisstein, Eric W. "Polyhedral formula". mathworld.wolfram.com (英語).
- ^ 宮崎興二『4次元図形百科』丸善出版、2020年、83頁。ISBN 978-4-621-30482-2。
参考文献
編集関連文献
編集- H.S.M. Coxeter:
- H. S. M. Coxeter, M. S. Longuet-Higgins and J. C. P. Miller: Uniform Polyhedra, Philosophical Transactions of the Royal Society of London, Londne, 1954
- Coxeter, H. S. M. (1973), Regular Polytopes (3rd ed.), New York: Dover Publications, ISBN 978-0-486-61480-9
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
- J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation [2]
外部リンク
編集- Weisstein, Eric W. "Polychoron". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Regular polychoron". mathworld.wolfram.com (英語).