正単体

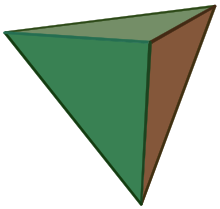
正単体（せいたんたい、regular simplex）は、2次元の正三角形、3次元の正四面体、4次元の正五胞体を各次元に一般化した正多胞体。なお、0次元正単体は点、1次元正単体は線分である。

2次元正単体（正三角形）

3次元正単体（正四面体）

4次元正単体（正五胞体）の投影図

また言い換えると、単体である正多胞体、つまり、辺の長さが全て等しい単体である。

$\alpha$体（アルファたい）ともいい、n (n ≥ 0) 次元正単体を $\alpha _{n}$ と書く。

超立方体（正測体）、正軸体と並んで、5次元以上での3種類の正多胞体の1つである。

作図

n 次元正単体は、n + 1 次元空間内で作図するのが簡単である。$(1,0,0,\cdots ,0)$ の巡回

$(1,0,0,\cdots ,0),(0,1,0,\cdots ,0),\cdots ,(0,0,\cdots ,0,1)$

を頂点として、互いを辺で結べばよい。この図形は、原点を中心とするn + 1 次元正軸体の n 次元面の一つである。例えば (1, 0, 0), (0, 1, 0), (0, 0, 1)を頂点とする正三角形（2次元正単体）は (0, 0, 0)を中心とする正八面体（3次元正軸体）の面の一つであるが、この場合は (1, 1, 1)を4番目の頂点とする正四面体の構成面でもあり、2種類の正多面体で空間充填が可能である。

n 次元空間内で作図するには、

• 座標変換する。
• n - 1 次元単体を作図し、重心で直交する垂線上の適切な位置に頂点を追加する。
• 自明な0次元単体から開始し、再帰的に1つ上の次元の正単体を作図する。

などがある。

性質

特にことわらない限り、辺の長さが a の n 次元正単体について述べる。

超体積は、

${\frac {\sqrt {n+1}}{n!{\sqrt {2^{n}}}}}a^{n}$

超表面積は

${\frac {(n+1){\sqrt {n}}}{(n-1)!{\sqrt {2^{n-1}}}}}a^{n-1}$

である。

ファセット (n - 1 次元面) は n - 1 次元正単体である。したがって一般に、m (0 ≤ m ≤ n - 1) 次元面は m 次元正単体である。たとえば、正五胞体（4次元正単体）の面（2次元面）は正三角形（2次元正単体）、胞（3次元面）は正四面体（3次元正単体）である。

m 次元面の個数は

${}_{n+1}\operatorname {C} _{m+1}$

である。これはパスカルの三角形の第 n + 2 段の m + 2 番目の数字である。特に、頂点とファセットはそれぞれ $n+1$ 個である。

m (0 ≤ m ≤ n - 2) 次元面に集まるl (m + 1 ≤ l ≤ n - 1) 次元面の個数は

${}_{n-m}\operatorname {C} _{l-m}$

である。これはパスカルの三角形の第 n - m + 1 段の l - m + 1 番目の数字であり、n - m - 1 次元単体の l - m - 1 次元面の個数である。

自らと双対である。

ペトリー多胞体は n - 1 次元正軸体である。たとえば、正四面体のペトリー多角形は正方形である。

関連項目

• 単体 (数学)