斜方二十・十二面体

斜方二十・十二面体（しゃほうにじゅうじゅうにめんたい、英: rhombicosidodecahedron）、または菱形二十・十二面体（りょうけいにじゅうじゅうにめんたい）、小菱形二十・十二面体（しょうりょうけいにじゅうじゅうにめんたい、英: small rhombicosidodecahedron）、切頂菱形三十面体（せっちょうりょうけいさんじゅうめんたい、英: truncated rhombic triacontahedron）とは、半正多面体の一種で、正十二面体または正二十面体の辺を削ったような立体である。菱形三十面体の各頂点を辺の中心まで切り落とした形でもある。二十・十二面体の各頂点を辺の中心まで切り落としたような形にもなっているが、正確ではない。

斜方二十・十二面体
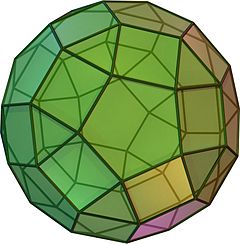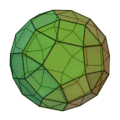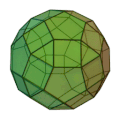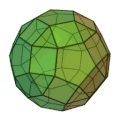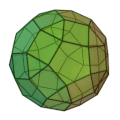種別	半正多面体
面数	62
面形状	正三角形: 20 正方形: 30 正五角形: 12
辺数	120
頂点数	60
頂点形状	3, 4, 5, 4（正三角形1枚と正方形2枚と正五角形1枚が3,4,5,4の順に集まる）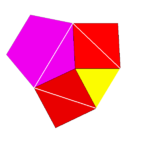
シュレーフリ記号	rr{5, 3} rsr{3, 3}
ワイソフ記号	3 5 | 2
対称群	Ih
双対多面体	凧形六十面体
特性	凸集合
展開図の例

菱形二十・十二面体という呼称の「菱形」は、菱形三十面体に由来する面を持つ事に由来する。

性質

斜方二十・十二面体は正十二面体（青い面）、もしくは正二十面体（赤い面）を膨張させた形をしている

赤い面は正十二面体由来、青い面は正二十面体由来、黄色い面は菱形三十面体由来

• 表面積: 一辺を$a$とすると $S=(30+5{\sqrt {3}}+3{\sqrt {25+10{\sqrt {5}}}})a^{2}$
• 外接球半径: 一辺を2とすると${\sqrt {11+4{\sqrt {5}}}}$
• ゾムのノードはこの立体の正方形を長方形に変形させた形をしている。
• 正五角台塔を最大3つまで取り出せる。

頂点が共通となる立体

正確

• 
  小十二・二十・十二面体
• 
  小斜方十二面体
• 
  小星型切頂十二面体
• 
  6個のアルキメデスの星型五角柱による複合多面体
• 
  12個のアルキメデスの星型五角柱による複合多面体

不正確

• 
  切頂大二十面体
• 
  小二十・二十・十二面体
• 
  小二重三角十二・二十・十二面体
• 
  小十二・二十面体
• 
  大星型切頂十二面体
• 
  大変形十二・二十・十二面体
• 
  大二重斜方二十・十二面体
• 
  大二重変形二重斜方十二面体
• 
  20個の正八面体の複合多面体
• 
  20個の四面半六面体の複合多面体

近縁な立体

一様多面体

• 
  二十・十二面体
  r{5, 3}
  （ベースの形）
• 
  斜方切頂二十・十二面体
  tr{5, 3}
  （二十・十二面体からの変形の中間段階にあたる）
• 
  変形十二面体
  sr{5, 3}
  （菱形三十面体由来の正方形を、特定の規則で正三角形2枚に置き換える）
• 
  一様大斜方二十・十二面体
  rr{5/3, 3}
• 
  菱形三十面体
  r{5, 3}
  （ベースの形2）

ジョンソンの立体

• 
  側台塔回転斜方二十・十二面体
  （正五角台塔を1つ回す）
• 
  側台塔欠損斜方二十・十二面体
  （正五角台塔を1つ取り除く）
• 
  正五角台塔

その他

• 
  斜方二十・十二面体と凧形六十面体による複合多面体

関連項目

• 斜方立方八面体 - 立方体または正八面体に対して同じ事を行ったもの
• 斜方十二・十二面体 - 小星型十二面体または大十二面体に対して同じ事を行ったもの

外部リンク

• Weisstein, Eric W. "斜方二十・十二面体". mathworld.wolfram.com (英語).