中点三角形
中点三角形（ちゅうてんさんかくけい、英:medial triangle, midpoint triangle）または補三角形[1]、中三角形[2]は、三角形の3辺の中点を頂点とする三角形である。
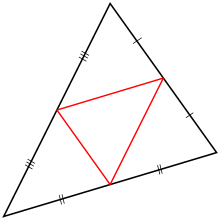
性質
編集中点三角形の3辺の長さは元の三角形の半分である。これは中点連結定理から容易に導かれる。これより、中点三角形と元の三角形は相似であり、その比は 1:2 であることが分かる。また、相似の中心は重心（2つの三角形の重心は一致する）である。
元の三角形に対する中点三角形のように、重心を中心に-1/2拡大した図形を、元の図形の「Complement」と言う。以下の表もComplementの一例である[3]。
元の三角形との対応関係
編集| 中点三角形 | 元の三角形 |
|---|---|
| 頂点 | 辺の中点 |
| 重心 | 重心 |
| 内心 | シュピーカー点 |
| 外心 | 九点円の中心 |
| 垂心 | 外心 |
| ジェルゴンヌ点 | ミッテンプンクト |
| ナーゲル点 | 内心 |
| ド・ロンシャン点 | 垂心 |
| 第三ブロカール点 | ブロカール中点 |
| オイラー線 | オイラー線 |
| 外接円 | 九点円 |
| 内接円 | シュピーカー円 |
| シュタイナーの外接楕円 | シュタイナーの内接楕円 |
座標
編集
逆補三角形
編集逆補三角形[1]（Anticomplementary triangle[5]）または反中点三角形[6]とは三角形ABCを中点三角形とする三角形である。元の三角形、中点三角形と相似である。英名の「Anticomplementary」は、逆補三角形の頂点が元の三角形のAnticomplement、重心を中心に-2倍に拡大した点であること（2:1の反転[7]）に由来する[8]。
逆補三角形は重心座標で以下の式で表される。
脚注
編集- ^ a b 『初等幾何学 第1巻 平面之部』山海堂書店、1913年、538頁。doi:10.11501/930885。
- ^ 『英和数学新字典』開新堂、1902年、184,311頁。doi:10.11501/826188。
- ^ Weisstein, Eric W.. “Complement” (英語). mathworld.wolfram.com. 2024年3月30日閲覧。
- ^ Weisstein, Eric W.. “Medial Triangle” (英語). mathworld.wolfram.com. 2024年7月13日閲覧。
- ^ Weisstein, Eric W.. “Anticomplementary Triangle” (英語). mathworld.wolfram.com. 2024年7月13日閲覧。
- ^ “三角形の心”. taurus.ics.nara-wu.ac.jp. 2024年7月13日閲覧。
- ^ 一松, 信 編『重心座標による幾何学』（初版）現代数学社、京都市、2014年、20頁。ISBN 978-4-7687-0437-0。
- ^ Weisstein, Eric W.. “Anticomplement” (英語). mathworld.wolfram.com. 2024年3月30日閲覧。
 | この項目は、初等幾何学に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています。 |