長六度
長六度は西洋の音楽理論一般に発生する2つの六度の半音大きい方である。長六度は9半音であるが、一方の小さい方の六度である短六度は8半音である。 2つのうち大きい方であるため、長六度は長音程である。例えば、Cから最も近いAまでの間隔は長六度となる。

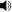 Play
Play
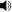 Play、Cの3ピタゴラス完全五度。
Play、Cの3ピタゴラス完全五度。長六度音程は短三和音の第1転回形、長三和音の第2転回形、減三和音の任意の転回形で発生する。また、属七の和音の第2転回形と第3転回形でも発生する。
長六度の周波数比
編集さまざまな調律において「長六度」と呼ばれる音程が存在し、それぞれ修飾語をつけて音程の違いが区別されることがある。以下の例ではセント値が小さいものから列挙する。
関連項目
編集脚注
編集- ^ Alexander J. Ellis, Additions by the translator to Hermann L. F. Von Helmholtz (2007). On the Sensations of Tone, p.456. ISBN 978-1-60206-639-7.
| 長六度 | ||||||
|---|---|---|---|---|---|---|
| 半音 | インターバルクラス | 平均律におけるセント | 全音階に基づく名前 | 純正律における振動数比 | 純正律におけるセント | 平均律と純正律のセント差 |
| 9 | 3 | 900 cents | 長六度 | 5:3 | 884 | -16 cents |
| そのほかの音程 | ||||||
| 一度 - 短二度 - 長二度 - 短三度 - 長三度 - 完全四度 - 増四度 - 減五度 - 完全五度 - 短六度 - 長六度 - 短七度 - 長七度 - 八度 | ||||||