立方体グラフ
数学のグラフ理論の分野における立方体グラフ(りっぽうたいグラフ、英: cubic graph)とは、すべての頂点の次数が 3 であるようなグラフのことを言う。言い換えると、立方体グラフとは 3-正則グラフである。立方体グラフは 3価グラフとも呼ばれる。2部立方体グラフ(bicubic graph)とは、立方体グラフかつ2部グラフであるようなグラフのことを言う。
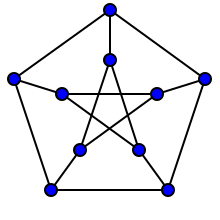
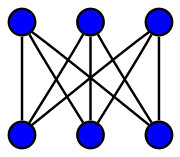
対称性
編集1932年、ロナルド・フォスターは、フォスター調査(Foster census)の皮切りとして、立方体対称グラフの例の集計をはじめた[1]。設備グラフやピーターセングラフ、ヒーウッドグラフ、メビウス-カントールグラフ、パップスグラフ、デザルググラフ、ナウルグラフ、コクセターグラフ、トゥッテ-コクセターグラフ、ディックグラフ、フォスターグラフ、ビッグス-スミスグラフなど、多くの有名なグラフは立方体かつ対称的であった。
ウィリアム・トーマス・タットは、長さ s の各二つの有向路が、ちょうど一回のグラフの対称性によって互いに写される時、そのような s の最小のものによって対称立方体グラフを分類した。彼は、そのような s は多くとも 5 であることを示し、s が 1 から 5 であるような各グラフの例を提示した[2]。
半対称立方体グラフには、グレイグラフ(最小の半対称立方体グラフ)やリュブリャナグラフ、トゥッテ12-ケージが含まれる。
フルフトグラフは、対称性を持たない最小の立方体グラフの二つの内の一つである。それは、単一のグラフ自己同型として、恒等自己同型のみを備える。
彩色と独立集合
編集グラフ理論によると、完全グラフ K4 以外のすべての立方体グラフは、多くとも 3色によって彩色される。したがって、K4 以外のすべての立方体グラフは、少なくとも n/3 個の頂点の独立集合を持つことになる。ここで n はそのグラフ内の頂点の数とする:例えば、3-彩色における最大の色の類は、少なくともこのくらい多くの頂点を含む。
ビジングの定理によると、すべての立方体グラフは、その辺彩色のために 3色か 4色を必要とする。3-辺彩色はテイト彩色として知られ、そのグラフの辺を三つの完全マッチングへと区分する。ケーニヒの線彩色定理によれば、すべての2部立方体グラフにはテイト彩色が存在する。
テイト彩色が存在しない、橋のない立方体グラフはスナークとして知られる。ピーターセングラフや、ティーツェのグラフ、ブラヌサスナーク、フラワースナーク、ダブルスタースナーク、スゼッケルスナーク、ワトキンススナークなどが、これに該当する。スナークは無数に存在する[3]。
位相と幾何
編集立方体グラフは位相幾何学の分野において、いくつかの方法によって自然に現れる。例えば、1-次元CW複体であるようなグラフを考えた時、立方体グラフは、そのグラフの 0-スケルトンと最大 1-セル接着写像が互いに素であるようなジェネリック(generic)である。立方体グラフはまた、どの頂点においても三つの面が接している正十二面体のような、三次元における単純多面体のグラフとして構成される。
二次元平面上の任意のグラフ埋め込みは、graph-encoded map として知られる立方体グラフの構造によって表現される。この構造において、立方体グラフの各頂点は埋め込みの旗、すなわち、互いに付帯した頂点、辺および平面の表面からなる組を表す。各旗の三つの隣(neighbor)は、その組の内のどれか一つを変更し、他の二つはそのままにしたものとして得られるような三つの旗である[4]。
ハミルトン性
編集立方体グラフのハミルトン性については多くの研究結果がある。1980年にP.G. テイトは、すべての立方多面体グラフはハミルトン閉路を持つと予想した。このテイトの予想に対する反例は、ウィリアム・トーマス・トゥッテの 46-頂点タットグラフによって、1946年に挙げられた。そのトゥッテは 1971年、すべての 2部立方体グラフはハミルトンであると予想した。しかし、ジョセフ・ホートンは 96-頂点ホートングラフをこの反例として挙げた[5]。その後、マーク・エリンガムはさらに二つの反例を挙げた:エリンガム-ホートングラフである[6][7]。未だに解決のなされていない、テイトとトゥッテの予想の組合せであるバーネットの予想では、すべての二部立方多面体グラフはハミルトンである、としている。立方体グラフがハミルトンであるとき、LCF表記によってそれを正確に表現することが出来る。
すべての n-頂点立方体グラフの中から一様にランダムに一つの立方体グラフが選ばれるとき、それはハミルトンであることが非常に多い: n が無限大へと向かう極限において、n-頂点立方体グラフがハミルトンである割合は 1 となる[8]。
デビッド・エプシュタインは、すべての n-頂点立方体グラフは多くとも 2n/3 個(およそ 1.260n 個)の異なるハミルトン閉路を含むと予想し、そのような多くの閉路を含む立方体グラフの例を提供した[9]。異なるハミルトン閉路の数について証明された最良の上界は、1.276n である[10]。
他の性質
編集任意の n-頂点立方体グラフのパス幅は、最大でも n/6 である。しかし、立方体グラフのパス幅の知られている下界のうち最良のものは、より小さく、0.082n である[11]。
グラフ理論を初めて扱った、1736年のレオンハルト・オイラーによる論文の一部分において証明された握手補題によると、すべての立方体グラフの頂点の数は偶数であることが分かる。
ジュリウス・ピーターセンの定理は、橋の無いすべての立方体グラフには完全マッチングが存在する、というものである[12]。
ロヴァースとプラマーは、すべての橋の無い立方体グラフには、指数関数的な数の完全マッチングが存在すると予想した。この予想は近年、すべての橋の無い n 頂点立方体グラフには少なくとも 2n/3656 個の完全マッチングが存在する、という結果とともに証明された[13]。
アルゴリズムと計算量
編集何人かの研究者は、立方体グラフに限定された指数関数時間アルゴリズムの計算量についての研究を行っている。例えば、グラフのパス分解に動的計画法を適用することにより、Fomin と Høie は時間 O(2n/6 + o(n)) 内に彼らの最大独立集合を見つける方法を示した[11]。巡回セールスマン問題は、立方体グラフによって時間 O(1.251n) 内に解くことが出来る[14]。
いくつかの重要なグラフ最適化問題はAPX困難である。すなわち、それらには近似率がある定数で評価されるような近似アルゴリズムが存在するが、(P=NPでない限り)近似率が 1 へと向かうような多項式時間近似スキームは存在しない。そのような問題には、最小の頂点被覆を見つける問題や最大独立集合、最小支配集合、最大カットを見つける問題などが含まれる[15]。立方体グラフの交叉数(任意のグラフ描画において交叉する辺の最小数)もまた、NP困難であるが、近似出来ることもある[16]。
出典
編集- ^ Foster, R. M. (1932), “Geometrical Circuits of Electrical Networks”, Transactions of the American Institute of Electrical Engineers 51 (2): 309–317, doi:10.1109/T-AIEE.1932.5056068.
- ^ Tutte, W. T. (1959), “On the symmetry of cubic graphs”, Canad. J. Math 11: 621–624, doi:10.4153/CJM-1959-057-2.
- ^ Isaacs, R. (1975), “Infinite families of nontrivial trivalent graphs which are not Tait colorable”, American Mathematical Monthly 82 (3): 221–239, doi:10.2307/2319844, JSTOR 2319844.
- ^ Bonnington, C. Paul; Little, Charles H. C. (1995), The Foundations of Topological Graph Theory, Springer-Verlag.
- ^ Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications. New York: North Holland, p. 240, 1976.
- ^ Ellingham, M. N. "Non-Hamiltonian 3-Connected Cubic Partite Graphs."Research Report No. 28, Dept. of Math., Univ. Melbourne, Melbourne, 1981.
- ^ Ellingham, M. N.; Horton, J. D. (1983), “Non-Hamiltonian 3-connected cubic bipartite graphs”, Journal of Combinatorial Theory, Series B 34 (3): 350–353, doi:10.1016/0095-8956(83)90046-1.
- ^ Robinson, R.W.; Wormald, N.C. (1994), “Almost all regular graphs are Hamiltonian”, Random Structures and Algorithms 5 (2): 363–374, doi:10.1002/rsa.3240050209.
- ^ Eppstein, David (2007), “The traveling salesman problem for cubic graphs”, Journal of Graph Algorithms and Applications 11 (1): 61–81, arXiv:cs.DS/0302030.
- ^ Gebauer, H. (2008), “On the number of Hamilton cycles in bounded degree graphs”, Proc. 4th Workshop on Analytic Algorithmics and Combinatorics (ANALCO '08).
- ^ a b Fomin, Fedor V.; Høie, Kjartan (2006), “Pathwidth of cubic graphs and exact algorithms”, Information Processing Letters 97 (5): 191–196, doi:10.1016/j.ipl.2005.10.012.
- ^ Petersen, Julius Peter Christian (1891), “Die Theorie der regulären Graphs (The theory of regular graphs)”, Acta Mathematica 15 (15): 193–220, doi:10.1007/BF02392606.
- ^ Esperer, Louis; Kardoš, František; King, Andrew D.; Král, Daniel; Norine, Serguei (2011), “Exponentially many perfect matchings in cubic graphs”, Advances in Mathematics 227 (4): 1646–1664, doi:10.1016/j.aim.2011.03.015.
- ^ Iwama, Kazuo; Nakashima, Takuya (2007), “An Improved Exact Algorithm for Cubic Graph TSP”, Computing and Combinatorics, Lecture Notes in Computer Science, 4598, Springer-Verlag, pp. 108–117, doi:10.1007/978-3-540-73545-8_13, ISBN 978-3-540-73544-1.
- ^ Alimonti, Paola; Kann, Viggo (2000), “Some APX-completeness results for cubic graphs”, Theoretical Computer Science 237 (1–2): 123–134, doi:10.1016/S0304-3975(98)00158-3.
- ^ Hliněný, Petr (2006), “Crossing number is hard for cubic graphs”, Journal of Combinatorial Theory, Series B 96 (4): 455–471, doi:10.1016/j.jctb.2005.09.009.
関連項目
編集外部リンク
編集- Weisstein, Eric W. "Bicubic Graph". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Cubic Graph". mathworld.wolfram.com (英語).
