球面三角法

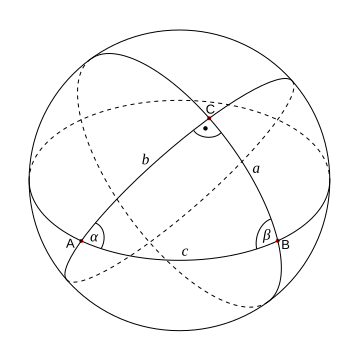
球面三角法（きゅうめんさんかくほう、英: spherical trigonometry）とは、いくつかの大円で囲まれた球面上の図形（球面多角形、とくに球面三角形）の辺や角の三角関数間の関係を扱う球面幾何学の一分野である。 球面上に2点A,Bがあるとき、この2点と球の中心を通る平面で切断したときの断面に現れる円が大円であり、このときの大円上の弧ABを球面多角形においては辺と呼ぶ。 通常、球の半径は1とするので、辺の長さはその辺を含む大円における中心角の弧度法表示と一致する。 平面三角法では6つの要素のうち3つの要素が決定されれば、残りの3つの要素を求めることができる。球面三角法でも同様に、3つの要素が分かれば残りの3つの要素を求めることができる。

球面三角形

球面三角法は、主に天文学や航海術で利用されてきた。現在では電子計算機の発達により、より簡潔に式を表すことができる行列を使用した座標変換に計算方法が移行している。

球面三角法の基本公式

ABC を球面三角形とし辺 BC, CA, AB の長さをそれぞれ a, b, c とする。弧 AB を含む大円が乗る平面と弧 AC を含む大円が乗る平面のなす角を A とする。これは、点 A における2つの大円の接ベクトルのなす角ともいえる。ただし、a と一致するとは限らない。同様に B, C も定義する。 このとき、次の式が成り立つ。

球面三角法の余弦定理

${\begin{aligned}\cos a&=\cos b\cos c+\sin b\sin c\cos A\\\cos b&=\cos c\cos a+\sin c\sin a\cos B\\\cos c&=\cos a\cos b+\sin a\sin b\cos C\end{aligned}}$

球面三角法の正弦定理

${\frac {\sin a}{\sin A}}={\frac {\sin b}{\sin B}}={\frac {\sin c}{\sin C}}$

正弦余弦定理

${\begin{aligned}\sin a\cos B&=\cos b\sin c-\sin b\cos c\cos A\\\sin a\cos C&=\cos c\sin b-\sin c\cos b\cos A\end{aligned}}$

球面三角法の正接定理

${\frac {\tan {\dfrac {A+B}{2}}}{\tan {\dfrac {A-B}{2}}}}={\frac {\tan {\dfrac {a+b}{2}}}{\tan {\dfrac {a-b}{2}}}}$

球面三角法の余接定理

$\cot a\sin b=\cos b\cos C+\cot A\sin C$

面積（球面の半径 $=r$，球過量 (Spherical Excess) $=E$，$2s=a+b+c$）

球面三角形ABCの面積 $=Er^{2}$

${\begin{aligned}E&=A+B+C-\pi \\&=4\tan ^{-1}{\sqrt {\tan {\frac {s}{2}}\tan {\frac {s-a}{2}}\tan {\frac {s-b}{2}}\tan {\frac {s-c}{2}}}}\\&=2\sin ^{-1}{\frac {\sqrt {\sin s\sin(s-a)\sin(s-b)\sin(s-c)}}{2\cos {\dfrac {a}{2}}\cos {\dfrac {b}{2}}\cos {\dfrac {c}{2}}}}\\&=2\cos ^{-1}{\frac {1+\cos a+\cos b+\cos c}{4\cos {\dfrac {a}{2}}\cos {\dfrac {b}{2}}\cos {\dfrac {c}{2}}}}\end{aligned}}$

第1式をジラールの式、第2式をリュイリエの式、第3式をカニョリの式、第4式をオイラーの式という。

誘導定理

$2s=a+b+c$ 、 $2S=A+B+C$ とおく。

${\begin{aligned}\sin {\frac {A}{2}}&={\sqrt {\frac {\sin(s-b)\sin(s-c)}{\sin b\sin c}}}\\\cos {\frac {A}{2}}&={\sqrt {\frac {\sin s\sin(s-a)}{\sin b\sin c}}}\\\tan {\frac {A}{2}}&={\sqrt {\frac {\sin(s-b)\sin(s-c)}{\sin s\sin(s-a)}}}\end{aligned}}$

${\begin{aligned}\sin {\frac {a}{2}}&={\sqrt {\frac {-\cos S\cos(S-A)}{\sin B\sin C}}}\\\cos {\frac {a}{2}}&={\sqrt {\frac {\cos(S-B)\sin(S-C)}{\sin B\sin C}}}\\\tan {\frac {a}{2}}&={\sqrt {\frac {-\cos S\cos(S-A)}{\cos(S-B)\cos(S-C)}}}\end{aligned}}$

直角球面三角形

天文学や航海術では一つの角が直角の場合が多く、この場合公式は簡単になる。

$C={\frac {\pi }{2}}$ とすると、

${\begin{alignedat}{4}&{\text{(R1)}}&\qquad \cos c&=\cos a\,\cos b,&\qquad \qquad &{\text{(R6)}}&\qquad \tan b&=\cos A\,\tan c,\\&{\text{(R2)}}&\sin a&=\sin A\,\sin c,&&{\text{(R7)}}&\tan a&=\cos B\,\tan c,\\&{\text{(R3)}}&\sin b&=\sin B\,\sin c,&&{\text{(R8)}}&\cos A&=\sin B\,\cos a,\\&{\text{(R4)}}&\tan a&=\tan A\,\sin b,&&{\text{(R9)}}&\cos B&=\sin A\,\cos b,\\&{\text{(R5)}}&\tan b&=\tan B\,\sin a,&&{\text{(R10)}}&\cos c&=\cot A\,\cot B.\end{alignedat}}$

これらを記憶するためにネイピアの円がある。

ネイピアの円

ネイピアの円と直角球面三角形

右図をネイピアの円という。 ${\bar {a}}={\frac {\pi }{2}}-a,{\bar {b}}={\frac {\pi }{2}}-b$である。

ネイピアの円のどれか一つの要素を中央要素とし、その隣の要素を隣接要素、残りの中央要素の反対側にある2つの要素を対向要素とする。このとき上記の定理(R1)～(R10)は次のように書ける。

中央要素の余弦 = 隣接要素の余接の積

中央要素の余弦 = 対向要素の正弦の積

象限三角形

球面三角形の一辺が${\frac {\pi }{2}}$となっているものを象限三角形という。この場合も公式は簡単になる。$c={\frac {\pi }{2}}$とすると、

${\begin{alignedat}{4}&{\text{(Q1)}}&\qquad \cos C&=-\cos A\,\cos B,&\qquad \qquad &{\text{(Q6)}}&\qquad \tan B&=-\cos a\,\tan C,\\&{\text{(Q2)}}&\sin A&=\sin a\,\sin C,&&{\text{(Q7)}}&\tan A&=-\cos b\,\tan C,\\&{\text{(Q3)}}&\sin B&=\sin b\,\sin C,&&{\text{(Q8)}}&\cos a&=\sin b\,\cos A,\\&{\text{(Q4)}}&\tan A&=\tan a\,\sin B,&&{\text{(Q9)}}&\cos b&=\sin a\,\cos B,\\&{\text{(Q5)}}&\tan B&=\tan b\,\sin A,&&{\text{(Q10)}}&\cos C&=-\cot a\,\cot b.\end{alignedat}}$

象限三角形の場合はネイピアの円に ${\bar {A}},{\bar {B}},a,\pi -C,b$ を当てはめればよい。

極三角形と双対原理

球面三角形 ABC の極三角形 A'B'C'

一般に、大円の平面に垂直な直径の両端をその大円の極という。右図において球面三角形ABCの1つの辺BCを考えると、それには2つの極があるが、そのうち辺BCから見てAと同じ側にあるほうをA'とする。同様に辺CA, ABについても極B', C'を定めることができる。このようにして得られた3点A', B', C'を結んで新しい一つの球面三角形A'B'C'が得られる。これを元の球面三角形ABCの極三角形という。

球面三角形A'B'C'が球面三角形ABCの極三角形であるならば、逆に球面三角形ABCは球面三角形A'B'C'の極三角形である。また今、球面三角形A'B'C'が球面三角形ABCの極三角形であるとし、その三辺、三角をそれぞれa', b', c'、A', B', C'で表すと、a, b, c、A, B, Cとの間には次のような関係がある：

${\begin{alignedat}{3}A'&=\pi -a,&\qquad B'&=\pi -b,&\qquad C'&=\pi -c,\\a'&=\pi -A,&b'&=\pi -B,&c'&=\pi -C.\end{alignedat}}$

上記をまとめると、球面三角形の法則は、それぞれの要素の向かい合った要素の補角に置き換えても成り立つ。これを双対原理という。具体例を挙げると

$\cos a=\cos b\cos c+\sin b\sin c\cos A$

から

$\cos(\pi -A)=\cos(\pi -B)\cos(\pi -C)+\sin(\pi -B)\sin(\pi -C)\cos(\pi -a)$

すなわち

$\cos A=-\cos B\cos C+\sin B\sin C\cos a$

が成り立つ。

haversine 半正矢関数

→詳細は「半正矢関数の公式」を参照

半正矢関数 $\operatorname {hav}$は値は常に正であり、かつ、偶関数である：

$\operatorname {hav} x\ {\overset {\underset {\mathrm {def} }{}}{=}}\ {\frac {1}{2}}(1-\cos x)=\sin ^{2}{\frac {x}{2}}$

半正矢関数の公式は球面三角法の余弦定理から導出できる：

$\operatorname {hav} a\ =\operatorname {hav} (b-c)+\sin b\sin c\ \operatorname {hav} A$

これは航海用として、球面上の2点間の球面に沿った距離を求める際に用いられた。前述の余弦定理でも求めることは可能だが、2地点間が近い（例えば経度差が0に近い）とき $\cos {x}=0.99999999$ といった値を使うことになり、計算しづらいのでこちらを用いた。

この公式を用いると、球の2点の緯度が $\varphi _{1},\varphi _{2}$、経度が $\lambda _{1},\lambda _{2}$ であるとき、2点間の弧度 $\theta$ との関係式は、

$\operatorname {hav} \theta =\operatorname {hav} (\varphi _{2}-\varphi _{1})+\cos \varphi _{2}\cos \varphi _{1}\operatorname {hav} (\lambda _{2}-\lambda _{1})$

ここから求めた $\theta$ に地球半径約6371 kmを掛ければ、地球上でのおおよその距離が分かる。

ドランブル (Delambre) の公式

ジャン＝バティスト・ジョゼフ・ドランブルによる。ガウスの公式と呼ばれることもある。

${\begin{aligned}\cos {\frac {A+B}{2}}\cos {\frac {c}{2}}&=\cos {\frac {a+b}{2}}\sin {\frac {C}{2}}\\\sin {\frac {A+B}{2}}\cos {\frac {c}{2}}&=\cos {\frac {a-b}{2}}\cos {\frac {C}{2}}\\\cos {\frac {A-B}{2}}\sin {\frac {c}{2}}&=\sin {\frac {a+b}{2}}\sin {\frac {C}{2}}\\\sin {\frac {A-B}{2}}\sin {\frac {c}{2}}&=\sin {\frac {a-b}{2}}\cos {\frac {C}{2}}\end{aligned}}$

ネイピア (Napier) の公式

${\begin{aligned}\tan {\frac {A+B}{2}}={\frac {\cos {\dfrac {a-b}{2}}}{\cos {\dfrac {a+b}{2}}}}\cot {\frac {C}{2}}\\\tan {\frac {A-B}{2}}={\frac {\sin {\dfrac {a-b}{2}}}{\sin {\dfrac {a+b}{2}}}}\cot {\frac {C}{2}}\\\tan {\frac {a+b}{2}}={\frac {\cos {\dfrac {A-B}{2}}}{\cos {\dfrac {A+B}{2}}}}\tan {\frac {c}{2}}\\\tan {\frac {a-b}{2}}={\frac {\sin {\dfrac {A-B}{2}}}{\sin {\dfrac {A+B}{2}}}}\tan {\frac {c}{2}}\end{aligned}}$

脚注

参考文献

• 渡邊敏夫『数理天文学』恒星社厚生閣、1951年。 
• 長沢工『天体の位置計算』地人書館、1981年。 
• 河瀬和重「球面三角法の簡潔かつ体系的な理解への試み」『国土地理院時報』第132巻、国土地理院、2019年、115–118頁、doi:10.57499/JOURNAL_132_18。 

関連項目

• 球面幾何学
• 三角測量

外部リンク

• 『球面三角法』 - コトバンク
• Weisstein, Eric W. "Spherical Trigonometry". mathworld.wolfram.com (英語).
• Weisstein, Eric W. "Spherical Triangle". mathworld.wolfram.com (英語).