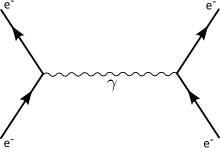
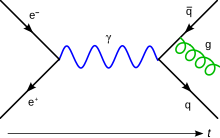
- 頂点(バーテックス、vertices):相互作用を表す。ラグランジアンにおける相互作用項の係数は一般に、相互作用を特徴付ける結合定数であり、頂点ではこの結合定数に比例する項が割り当てられる。
- 線:素粒子の伝搬を表す。線の種類で素粒子の種類を表す。相対論的量子力学の帰結として、全ての素粒子には粒子と反粒子が存在する。ファインマン・ダイアグラムの線は粒子と反粒子を、矢印を用いて同時に表す。
- 外線(external lines):ある頂点から出てそのままになっている線。考えている反応の始状態と終状態を表す。
- 内線(internal lines):ある頂点から出て別の頂点に入っている線。ある頂点の相互作用で作られ、別の頂点の相互作用で消される粒子、つまり量子力学的な仮想状態での粒子を表す。この意味で、内線で記述された粒子は質量殻条件を満たさない。
- 時間軸:時間軸がない場合は、頂点は時空間における点を表す。すなわち時空のあらゆる点(あらゆる場所、あらゆる時刻)での相互作用を表す図になっている。1つの時間軸の無いダイアグラムは、膨大な種類の時間軸が特定された過程の集まりになる。
ある始状態と終状態を決めた、すなわち外線を決めたとする。そこから無限個の頂点と内線を作り出せる、すなわち無限個のダイアグラムを作ることができ、無限個の仮想的な中間状態を考えなければならなくなる。そこで頂点の数を何個までと決めておけば、可能なダイアグラムの数は有限個になる。これを摂動論という。
ファインマンルールとは、与えられたラグランジアン密度からファインマンダイアグラムの
頂点、外線、内線のそれぞれに物理変数からなる因子(factor)を対応させるルールのことである。物理変数からなる因子とは、多くの場合ベクトル[要曖昧さ回避]やテンソルやスピノルである。
このルールに従い、それぞれのダイアグラムに対応する因子をかけ合わせて積分すると、
摂動的に、S行列から粒子の崩壊率(decay rate)、寿命、断面積(cross section)などの観測可能な物理量を計算することができる。
ファインマンルールには座標空間でのルールと運動量空間でのルールの2種類がある。
これらの対応表を与えるルールは、ある程度の一般的な形もあるが、通常、相互作用の形によってそれぞれ違った形のものが使われる。
一般的なファインマンルールの大雑把な計算の流れは次のように与えられる。
一般的なファインマンルールを用いたS行列の計算の流れ
編集
- 求めたい摂動の次数に等しいだけの頂点を持ったファインマンダイアグラムをすべて書き出す。この時、相互作用の形によって頂点から出る線の種類と数は決まっている。粒子と反粒子が異なるような場(実でない場)の場合、矢印で粒子の進行する向き(反粒子の進行とは逆方向)を示すことでこれを区別する。
- ファインマンルールに従い、頂点、内線、外線に対応する因子を全てかけ合わせ、積分を実行する。このときの積分は座標空間の場合、頂点に伴う座標変数について行い、運動量空間の場合は、内線に伴う運動量について行う。
- ダイアグラムに対称性がある場合は同じ形になるダイアグラムの個数で割る。(Symmetry factor)
- フェルミオンの反交換関係から出る符号(±)を掛ける。(fermionic sign)
- 書き出した全てのダイアグラムに対して足しあわせる。