ニュートン・ガウス線
幾何学において、ニュートン・ガウス線[1](ニュートン・ガウスせん、英: Newton–Gauss line, Gauss–Newton line)あるいは単にニュートン線[2]は、完全四辺形の3つの対角線の中点を結ぶ直線である。
凸四角形の2つの対角線の中点を結ぶ直線であるニュートン線とは区別される。四角形の辺を延長して、完全四辺形を作れば、四角形のニュートン線は完全四辺形のニュートン・ガウス線となる。
完全四辺形
編集一般の位置にある(どれも平行でないかつ共点でない)4つの直線は、完全四辺形を成す。この配置は4本の直線とその6つの交点から成る[3]。この6点のうち任意の2点を端点とする線分が、もと4直線の交点以外で交わるように、6つの交点を3組に分割することができる。この3つの線分を完全四辺形の対角線という。
ニュートン・ガウス線の存在証明
編集完全四辺形の対角線の中点が共線であることはとても有名な定理である[4]。証明方法も多く存在しており、例えば面積[4]や楔積[5]、ガウス・ボーデンミラーの定理[1]を用いるものなどがある。ここでは、1920年のHillyerによるメネラウスの定理を用いた証明を紹介する[6]。
対角線がAA', BB', CC'であるような完全四辺形ABCA'B'C'について、線分AA', BB', CC',BC, CA', A'Bの中点をそれぞれL, M, N, P, Q, Rとする。明らかにL, Q, Rは共線である。同様にM, R, PとN, P, Qも共線であるから、三角形の相似より次の関係式が成立する。
ただし、直線A’B'C と△ABC' にメネラウスの定理を用いて、3つの式の右辺の積は-1となる。したがって左辺の積は-1となるから、△PQRにメネラウスの定理の逆を使用して、点 L, M, Nは共線である。
円に内接する四角形への応用
編集BarbuとPatrascuによる、円に内接する四角形から作られる完全四辺形のニュートン・ガウス線を用いた定理を挙げる[7]。
等しい角
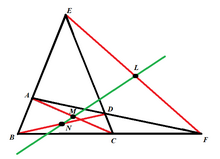
編集円に外接する四角形ABCDの対角線AC, BDの交点をF、対辺AB, CDの交点をE、 EFの中点をN、BCの中点をMとする(図1)。
定理
編集BFの中点をPとすれば、完全四辺形ABCDEFのニュートン・ガウス線と直線PMによって決定される角∠PMNは∠EFDと等しい。
証明
編集BE ∥ PNとFC ∥ PMから∠NPM = ∠EACが分かる。また、 である。
円に外接する四角形の性質より、
したがって∠NPM = ∠EDF。
R1, R2を△EDB, △FCDの外接円の半径として、正弦定理を使用することにより、
BE = 2 · PN と FC = 2 · PMより 。△PMN, △DFEの相似から∠NMP = ∠EFD。
備考
編集FCの中点をQとすれば、同様にして∠NMQ = ∠EFAが成立する。
等角共役線
編集定理
編集完全四辺形ABCDEFのニュートン・ガウス線のEを通る平行線は、∠BECにおける直線EFの等角共役線である[7]。
証明
編集三角形△EDF, △NPM は相似であるから、∠DEF = ∠PNMである。完全四辺形ABCDEFのニュートン・ガウス線NMのEを通る平行線とBCの交点をE'とする。
PN ∥ BE と NM ∥ EE' より、∠BEF = ∠PNF, ∠FNM = ∠E'EF。
したがって、
ニュートン・ガウス線を共有する2つの共円四角形
編集補題
編集GとHを、点Fのそれぞれ直線AB,CDにおける直交射影とする。
証明
編集前項で示したように、∠EFD = ∠PMN。 点PとNはそれぞれ直角三角形△BFG, △EFGの外心であるから∠PGF = ∠PFGと∠FGN = ∠GFNが成立する。
したがって、
よってMPGNは円に内接する。同様にして、MQHNも円に内接する。
定理
編集GF, HFの延長線は、それぞれEC, EBとI, Jで交わるとする。
完全四辺形 EFGHIJ, ABCDEFのニュートン・ガウス線は一致する[7]。
証明
編集2つの完全四辺形は対角線EFを共有する。Nは双方のニュートン・ガウス線上に位置する。四角形EGFHが円に内接することと、その円の中心がNであることより、NはG,Hと等距離である。
△GMP, △HMQ が合同ならば、MはHGの垂直二等分線上に位置するから、 直線MNは線分GHの中点を含むみ、完全四辺形EFGHIJのニュートン・ガウス線となる。
△GMP, △HMQの合同を示す。BF, BCの中点がM, Pであることより、PMQFは平行四辺形である。
したがって
更に、
よって、
したがって、二辺夾角相等より△GMPは △HMQは合同。
備考
編集△GMP, △HMQが合同であることから、 MPGN, MQHNの外接円も合同である。
他の性質
編集歴史
編集ニュートン・ガウス線はアイザック・ニュートンとカール・フリードリヒ・ガウスの名を冠する[要出典]。この定理の最初の枠組みはニュートン線における定理、ニュートンの定理であり、ニュートンは四角形に内接する円錐曲線の中心はニュートン・ガウス線上にあることを示した[9]。
ガウスとボーデンミラー(Bodenmiller)は、完全四辺形の対角線を直径とする3つの円は共軸であることを示した(ガウス・ボーデンミラーの定理)[10]。
出典
編集- ^ a b Evan Chen 著、兒玉太陽, 熊谷勇輝, 宿田彩人, 平山楓馬 訳『数学オリンピック幾何への挑戦 ユークリッド幾何学をめぐる船旅』日本評論社、2023年3月10日、274頁。ISBN 9784535789784。
- ^ a b 窪田忠彦『幾何学の基礎 第3版 (岩波全書 ; 第104)』岩波書店、1946年、102頁。doi:10.11501/1211294。
- ^ Alperin, Roger C. (6 January 2012). “Gauss–Newton Lines and Eleven Point Conics”. Research Gate. 2024年11月16日閲覧。
- ^ a b Johnson 2007, p. 62
- ^ Pedoe, Dan (1988) [1970], Geometry A Comprehensive Course, Dover, pp. 46–47, ISBN 0-486-65812-0
- ^ Johnson 2007, p. 152
- ^ a b c d Patrascu. “Some Properties of the Newton–Gauss Line”. Forum Geometricorum. 29 March 2023時点のオリジナルよりアーカイブ。29 April 2019閲覧。
- ^ 森本清吾『初等幾何学』朝倉書店、1953年、50,76頁。NDLJP:1372292。
- ^ Wells, David (1991), The Penguin Dictionary of Curious and Interesting Geometry, Penguin Books, p. 36, ISBN 978-0-14-011813-1
- ^ Johnson 2007, p. 172
参考文献
編集- JohnsonRoger A.『Advanced Euclidean Geometry』Dover、2007年(原著1929年)。ISBN 978-0-486-46237-0。
- (オンライン版) Johnson (1929年). “Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle”. HathiTrust. 28 May 2019閲覧。"Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle". HathiTrust. Retrieved 28 May 2019.
- Dorin Andrica; C. Turcas, George (2021). “The converse of the Newton-Gauss theorem”. INTERNATIONAL JOURNAL OF GEOMETRY.
外部リンク
編集- Bogomonly. “Theorem of Complete Quadrilateral: What is it?”. 11 May 2019閲覧。
- “QL-L1: The Newton Line”. EQF. 2024年11月16日閲覧。
- “Gauss line”. AoPS. 2024年11月16日閲覧。
- “Newton-Gauss line”. PlanetMath. 2024年11月16日閲覧。