スター (グラフ理論)
原文と比べた結果、この記事には多数の(または内容の大部分に影響ある)誤訳があることが判明しています。情報の利用には注意してください。 (2017年9月) |
この記事の正確性に疑問が呈されています。 |
スター もしくは星Sk は、グラフ理論の用語の1つであり、ただ1つの頂点とそれにつながる k 個の葉のみを持つグラフである。また、スターは完全2部グラフ K1, kでもある。スター Sk を直径が2で次数が k である木とする人も存在し、この場合 2 < k であり葉の数は k-1 である。
| スター | |
|---|---|
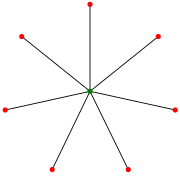 葉を7つ持つスター S7(一部の人はこれを S8と表現する) | |
| 頂点 | k+1 |
| 辺 | k |
| 直径 | min(2, k) |
| 内周 | ∞ |
| 彩色数 | min(2, k + 1) |
| 彩色指数 | k |
| 特性 |
頂点推移グラフ 木 (数学) 単位距離グラフ 2部グラフ |
| 表記 | Sk |
頂点が3個の星は特別にクローもしくは爪と呼ぶ。
スター Sk は k が偶数のときには edge-graceful であり、 k が奇数の場合はそうでない。スターは頂点推移グラフであり、 1 < k においてグラフの直径は2であり、内周は ∞ である。また、スターは自己同型群を持つ。すなわち、 k 次の対称群である。
スターは、(最大でも)1つの頂点の次数が1より大きい、連結グラフともいえる。
他のグラフとの関係
編集頂点数が3のスターであるクローはクローフリーグラフ(誘導部分グラフとしてクローを持たないグラフ)の定義で有名である[1][2]。また、ハスラー・ホイットニー (Hassler Whitney) のグラフ同型定理(一般的に、グラフ同型な線グラフはクローと三角形グラフ K3を除き同型である[3]。)の例外の1つでもある。
スターは木の特殊な場合であるため、木と同様にプリューファー列で表すことができ、スター Sk は中心の頂点を k-1 回並べた列となる[4]。
スターの考え方を用いて定義されているグラフ不変量がいくつかある。スターの樹化数は森に含まれる木が全てスターとなるような分割を行った際の最小の森の数として定義されている[5]。スター彩色数は、2つの色グループで彩色した場合、同じ色で接続された頂点グループが全てスターとなる彩色数である[6]。分枝幅が1であるというのは、連結している分枝がそれぞれスターであることと同値である[7]。
その他の用途
編集クローの頂点間の距離の集合は、任意の次元のユークリッド空間への等長写像を持たない、有限距離空間の一例となる[8]。
星型(スター型)のネットワーク・トポロジーはスターグラフでモデル化され、分散コンピューティングの分野において重要な概念である。
一定の長さの間隔で辺を識別することで形成したスターの幾何学的実現は、トロピカル幾何学の曲線の局所モデルとして使用される。トロピカル曲線は、スター型の距離空間の局所的に同型な距離空間として定義される。
参考文献
編集- ^ Faudree, Ralph; Flandrin, Evelyne; Ryjáček, Zdeněk (1997), “Claw-free graphs — A survey”, Discrete Mathematics 164 (1–3): 87–147, doi:10.1016/S0012-365X(96)00045-3, MR1432221.
- ^ Chudnovsky, Maria; Seymour, Paul (2005), “The structure of claw-free graphs”, Surveys in combinatorics 2005, London Math. Soc. Lecture Note Ser., 327, Cambridge: Cambridge Univ. Press, pp. 153–171, MR2187738
- ^ Whitney, Hassler (January 1932), “Congruent Graphs and the Connectivity of Graphs”, American Journal of Mathematics 54 (1): 150–168, doi:10.2307/2371086, JSTOR 2371086.
- ^ Gottlieb, J.; Julstrom, B. A.; Rothlauf, F.; Raidl, G. R. (2001), “Prüfer numbers: A poor representation of spanning trees for evolutionary search”, Proc. Genetic and Evolutionary Computation Conference, Morgan Kaufmann, pp. 343–350
- ^ Hakimi, S. L.; Mitchem, J.; Schmeichel, E. E. (1996), “Star arboricity of graphs”, Discrete Math. 149: 93–98, doi:10.1016/0012-365X(94)00313-8
- ^ Fertin, Guillaume; Raspaud, André; Reed, Bruce (2004), “Star coloring of graphs”, Journal of Graph Theory 47 (3): 163–182, doi:10.1002/jgt.20029.
- ^ Robertson, Neil; Seymour, Paul D. (1991), “Graph minors. X. Obstructions to tree-decomposition”, Journal of Combinatorial Theory 52 (2): 153–190, doi:10.1016/0095-8956(91)90061-N
- ^ Linial, Nathan (2002), “Finite metric spaces–combinatorics, geometry and algorithms”, Proc. International Congress of Mathematicians, Beijing, 3, pp. 573–586, arXiv:math/0304466