9項補題
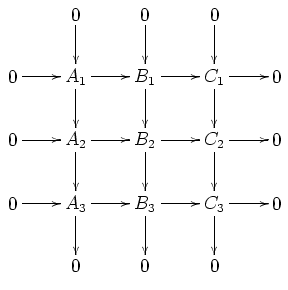
数学において、9項補題(英: nine lemma)、ナイン・レンマは、可換図式と完全列についてのステートメントで、任意のアーベル圏や群の圏において有効である。これは次のようなものである。下の図式
が可換図式であり、すべての列と下の2つの行が完全であれば、上の行もまた完全である。同様に、すべての列と上の2つの行が完全であれば、下の行もまた完全である。
9項補題は直接的な diagram chasing によって証明することができる。あるいは、蛇の補題を(1つ目のケースでは2つの下の行に対して、2つ目のケースでは上の2行に対して)適用することによっても証明できる。
Linderholm (p. 201) は9項補題の風刺的な見解を展開している。
- "Draw a noughts-and-crosses board... Do not fill it in with noughts and crosses... Instead, use curved arrows... Wave your hands about in complicated patterns over this board. Make some noughts, but not in the squares; put them at both ends of the horizontal and vertical lines. Make faces. You have now proved:
- (a) the Nine Lemma
- (b) the Sixteen Lemma
- (c) the Twenty-five Lemma..."
参考文献
編集- Linderholm, Carl (1971). Mathematics Made Difficult. Wolfe. ISBN 0-7234-0415-1