非圧縮性

連続体力学における非圧縮性（ひあっしゅくせい、英語: incompressibility）とは、連続体の密度が変形の前後で変化しないような性質を表す。連続体力学では質量保存則を考えるため、密度が一定であるならば体積も一定となる。非圧縮性を有する材料として、流体では河川を流れる水や音速を超えない範囲で運動している空気が挙げられる。これらを総称して、非圧縮性流体と呼んでいる。一方で、固体の場合は、ゴムに代表される超弾性体や降伏した金属などのような塑性体が挙げられる。

連続体力学
法則 質量保存の法則 運動量保存の法則 エネルギー保存の法則 クラウジウス–デュエムの不等式 固体力学 固体 · 変形 · 弾性 · 弾性波 · 弾塑性 · 塑性 · フックの法則 · 応力 · ひずみ · 有限変形理論 · レオロジー · 粘弾性 · 超弾性 流体力学 流体 · 流体静力学 流体動力学 · 粘度 · ニュートン流体 非ニュートン流体 表面張力 科学者 ニュートン · ストークス · ナビエ · コーシー · フック · ベルヌーイ

非圧縮性の定式化

図1.連続体の変形

連続体力学では、次に示す変形勾配テンソル$F$を用いて連続体の変形を考える。以後、使用する文字は図1に合わせた。

$d{\boldsymbol {x}}={\boldsymbol {F}}d{\boldsymbol {X}},\quad F_{ij}={\frac {\partial x_{i}}{\partial X_{j}}}$

ここで、${\boldsymbol {x}}$は変形形状$\kappa _{t}$内の位置を表し、${\boldsymbol {X}}$は基準形状（変形なし形状）$\kappa _{0}$内のもとの位置を表す。

さらに体積変化率$J$と変形勾配テンソル${\boldsymbol {F}}$に次の関係があることを利用する。

$J={\frac {dv}{dV}}=\det({\boldsymbol {F}})$

ここで、$dv$は変形形状$\kappa _{t}$内の微小六面体要素の体積を表し、$dV$は基準形状(変形なし形状)$\kappa _{0}$内の微小六面体要素の体積を表す。非圧縮性とは上記の体積変化率$J$が1であることに等しい、すなわち次のように定式化できる。

$J=\det({\boldsymbol {F}})=1$

流体力学との関連性

→「非圧縮性流れ」も参照

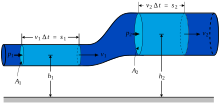
非圧縮性流体の基礎方程式のひとつに、次に示す連続の式がある。

$\mathrm {div} \,{\boldsymbol {v}}=0,\quad {\frac {\partial v_{j}}{\partial x_{j}}}=0$

これは、質量保存則および密度が一定であることを利用して導き出されるが、次のように体積変化率$J$の物質微分（物質時間導関数）を考えることでも導き出される。

${\frac {DJ}{Dt}}=J\mathrm {div} \,{\boldsymbol {v}}$

上式に$J=1$と${\frac {DJ}{Dt}}=0$を代入することで、連続の式が得られる。

なお、流体が非圧縮性であるか否かは流体の物性ではなく、流れの性質、具体的にはマッハ数による。

固体力学との関連性

固体力学において、体積ひずみという概念がある。ここでは、体積ひずみ$\epsilon _{V}$と体積変化率$J$との関連性について述べ、非圧縮性のもとで体積ひずみが0となることを示す。

変形勾配テンソル${\boldsymbol {F}}$は、変位勾配テンソル${\boldsymbol {H}}$と恒等テンソル${\boldsymbol {I}}$を用いると次のように表される。

${\boldsymbol {F}}={\boldsymbol {I}}+{\boldsymbol {H}},\quad F_{ij}=\delta _{ij}+H_{ij}$

ここで、変形勾配テンソル${\boldsymbol {H}}$は

$d{\boldsymbol {u}}={\boldsymbol {H}}d{\boldsymbol {X}},\quad H_{ij}={\frac {\partial u_{i}}{\partial X_{j}}}$

である。${\boldsymbol {u}}$は変位を表す。

変形勾配テンソル${\boldsymbol {F}}$の各要素は変位勾配テンソル（の成分）$H_{ij}$を用いると、以下の様に表される。

${\boldsymbol {F}}={\begin{pmatrix}1+H_{11}&H_{12}&H_{13}\\H_{21}&1+H_{22}&H_{23}\\H_{31}&H_{32}&1+H_{33}\end{pmatrix}}$

よって、体積変化率$J$を変位勾配テンソル$H_{ij}$で表すと、下の式を得る。

$J=\det(F)={\begin{vmatrix}1+H_{11}&H_{12}&H_{13}\\H_{21}&1+H_{22}&H_{23}\\H_{31}&H_{32}&1+H_{33}\end{vmatrix}}=1+H_{11}+H_{22}+H_{33}+H^{(2)}+H^{(3)}$

ここで、$H^{(2)}$ および $H^{(3)}$は変位勾配の2次の項と3次の項を表す。非圧縮性であることから、$J=1$とすると、結局次の式を得る。

$H_{11}+H_{22}+H_{33}+H^{(2)}+H^{(3)}=0$

微小変形を考えると、$H^{(2)}$と$H^{(3)}$が無視でき、

${\frac {\partial }{\partial X_{i}}}\approx {\frac {\partial }{\partial x_{i}}}$

となるため、次の式を得る。

$H_{11}+H_{22}+H_{33}={\frac {\partial u_{1}}{\partial X_{1}}}+{\frac {\partial u_{2}}{\partial X_{2}}}+{\frac {\partial u_{3}}{\partial X_{3}}}\approx {\frac {\partial u_{1}}{\partial x_{1}}}+{\frac {\partial u_{2}}{\partial x_{2}}}+{\frac {\partial u_{3}}{\partial x_{3}}}=\epsilon _{V}=0$

上記のように、非圧縮性から体積ひずみが0となることが示された。

参考文献

• 京谷孝史『よくわかる連続体力学ノート』森北出版、2008年12月。ISBN 978-4-627-94811-2。 

関連項目

• 圧縮性