超幾何分布 （ちょうきかぶんぷ、英 : hypergeometric distribution ）とは、成功状態をもつ母集団 から非復元抽出したときに成功状態がいくつあるかという確率 を与える離散確率分布 の一種である。男女・合否などのように2種の排他的属性に分割できる有限母集団からの非復元抽出に適用される。超幾何分布と対照的[ 注 1] 確率分布 には二項分布 がある。
超幾何分布
確率質量関数
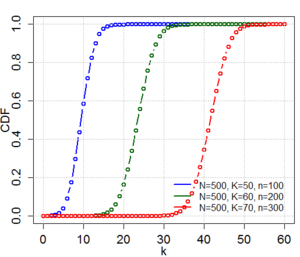
累積分布関数
母数
N
∈
{
0
,
1
,
2
,
⋯
}
K
∈
{
0
,
1
,
2
,
⋯
,
N
}
n
∈
{
0
,
1
,
2
,
⋯
,
N
}
{\displaystyle {\begin{aligned}N&\in \left\{0,1,2,\cdots \right\}\\K&\in \left\{0,1,2,\cdots ,N\right\}\\n&\in \left\{0,1,2,\cdots ,N\right\}\end{aligned}}}
台
{
max
{
0
,
n
+
K
−
N
}
,
⋯
,
min
{
n
,
K
}
}
{\displaystyle \left\{\max\{0,\,n+K-N\},\,\cdots ,\,\min\{n,\,K\}\right\}}
確率質量関数
(
K
k
)
(
N
−
K
n
−
k
)
(
N
n
)
{\displaystyle {\frac {{\binom {K}{k}}{\binom {N-K}{n-k}}}{\binom {N}{n}}}}
累積分布関数
1
−
(
n
k
+
1
)
(
N
−
n
K
−
k
−
1
)
(
N
K
)
3
F
2
[
1
,
k
+
1
−
K
,
k
+
1
−
n
k
+
2
,
N
+
k
+
2
−
K
−
n
;
1
]
,
{\displaystyle 1-{\frac {{\binom {n}{k+1}}{\binom {N-n}{K-k-1}}}{\binom {N}{K}}}\,{}_{3}\!F_{2}\!\!\left[{\begin{array}{c}1,\ k+1-K,\ k+1-n\\k+2,\ N+k+2-K-n\end{array}};1\right],}
p
F
q
{\displaystyle {}_{p}\!F_{q}}
一般超幾何関数 期待値
n
K
N
{\displaystyle n{K \over N}}
最頻値
⌊
(
n
+
1
)
(
K
+
1
)
N
+
2
⌋
{\displaystyle \left\lfloor {\frac {(n+1)(K+1)}{N+2}}\right\rfloor }
分散
n
K
N
N
−
K
N
N
−
n
N
−
1
{\displaystyle n{\frac {K}{N}}{\frac {N-K}{N}}{\frac {N-n}{N-1}}}
歪度
(
N
−
2
K
)
(
N
−
1
)
1
2
(
N
−
2
n
)
[
n
K
(
N
−
K
)
(
N
−
n
)
]
1
2
(
N
−
2
)
{\displaystyle {\frac {(N-2K)(N-1)^{\frac {1}{2}}(N-2n)}{[nK(N-K)(N-n)]^{\frac {1}{2}}(N-2)}}}
尖度
1
n
K
(
N
−
K
)
(
N
−
n
)
(
N
−
2
)
(
N
−
3
)
⋅
{\displaystyle \left.{\frac {1}{nK(N-K)(N-n)(N-2)(N-3)}}\cdot \right.}
[
(
N
−
1
)
N
2
(
N
(
N
+
1
)
−
6
K
(
N
−
K
)
−
6
n
(
N
−
n
)
)
+
{\displaystyle {\Big [}(N-1)N^{2}{\Big (}N(N+1)-6K(N-K)-6n(N-n){\Big )}+}
6
n
K
(
N
−
K
)
(
N
−
n
)
(
5
N
−
6
)
]
{\displaystyle 6nK(N-K)(N-n)(5N-6){\Big ]}}
モーメント母関数
(
N
−
K
n
)
2
F
1
(
−
n
,
−
K
;
N
−
K
−
n
+
1
;
e
t
)
(
N
n
)
{\displaystyle {\frac {{\binom {N-K}{n}}\scriptstyle {{}_{2}\!F_{1}(-n,-K;N-K-n+1;e^{t})}}{\binom {N}{n}}}}
特性関数
(
N
−
K
n
)
2
F
1
(
−
n
,
−
K
;
N
−
K
−
n
+
1
;
e
i
t
)
(
N
n
)
{\displaystyle {\frac {{\binom {N-K}{n}}\scriptstyle {{}_{2}\!F_{1}(-n,-K;N-K-n+1;e^{it})}}{\binom {N}{n}}}}
テンプレートを表示
超幾何分布 とは K 個の成功状態をもつ N 個の要素よりなる母集団 から n 個の要素を非復元抽出したときに k 個の成功状態が含まれている確率 を与える離散確率分布 の一種である。超幾何分布に従う確率変数 X の確率質量関数 fX は次で与えられる。
P
(
X
=
k
)
=
f
X
(
k
;
N
,
K
,
n
)
=
(
K
k
)
(
N
−
K
n
−
k
)
(
N
n
)
=
(
n
k
)
(
N
−
n
K
−
k
)
(
N
K
)
{\displaystyle \operatorname {P} (X=k)=f_{X}(k;N,K,n)={\frac {{\binom {K}{k}}{\binom {N-K}{n-k}}}{\binom {N}{n}}}={\frac {{\binom {n}{k}}{\binom {N-n}{K-k}}}{\binom {N}{K}}}}
確率質量関数は max{0, n + K − N } ≤ k ≤ min{K , n }
超幾何分布は N が大きくなると、二項分布 に近づく。また K / N n が大きいとき、ポアソン分布 に近づく。
期待値
E
(
X
)
=
n
⋅
K
N
{\displaystyle E(X)=n\cdot {\frac {K}{N}}}
分散
Var
(
X
)
=
n
⋅
K
N
⋅
N
−
K
N
⋅
N
−
n
N
−
1
{\displaystyle \operatorname {Var} (X)=n\cdot {\frac {K}{N}}\cdot {\frac {N-K}{N}}\cdot {\frac {N-n}{N-1}}}
最頻値
⌊
(
n
+
1
)
(
K
+
1
)
N
+
2
⌋
{\displaystyle \left\lfloor {\frac {(n+1)(K+1)}{N+2}}\right\rfloor }
対称性
f
X
(
k
;
N
,
K
,
n
)
=
f
X
(
k
;
N
,
n
,
K
)
=
f
X
(
n
−
k
;
N
,
N
−
K
,
n
)
=
f
X
(
K
−
k
;
N
,
K
,
N
−
n
)
{\displaystyle {\begin{aligned}f_{X}(k;N,K,n)&=f_{X}(k;N,n,K)\\&=f_{X}(n-k;N,N-K,n)\\&=f_{X}(K-k;N,K,N-n)\end{aligned}}}
例えば、赤い玉10個と白い玉20個を混ぜた、計30個の玉を入れた壺 の中から5個の球を取り出すとき、赤い玉がちょうど1つである確率は
(
10
1
)
(
30
−
10
5
−
1
)
(
30
5
)
=
8075
23751
≈
0.34
{\displaystyle {\frac {{\binom {10}{1}}{\binom {30-10}{5-1}}}{\binom {30}{5}}}={\frac {8075}{23751}}\approx 0.34}
赤い玉の個数の期待値は
5
×
10
30
≈
1.67
{\displaystyle {\frac {5\times 10}{30}}\approx 1.67}
元々、N個のビー玉が壺の中に入っていて、そのうち緑玉がK個、赤玉はN-K個であったとする。この中から（目を瞑って）n個のビー玉を非復元抽出 で取り出したとする。このとき、（n回の試行のうち）緑玉がk回取り出される確率を求めたい。 なお、壺には緑玉と赤玉以外には入っておらず、同色同士の玉は区別できないものとする。
この問題において、「成功」を「緑玉」に、「失敗」を「赤玉」例えることで、超幾何分布の問題に帰着でき、k回成功する確率(即ち、k回緑玉が取り出される確率)は、以下のようになる。
P
(
X
=
k
)
=
f
(
k
;
N
,
K
,
n
)
=
(
K
k
)
(
N
−
K
n
−
k
)
(
N
n
)
.
{\displaystyle P(X=k)=f(k;N,K,n)={{{K \choose k}{{N-K} \choose {n-k}}} \over {N \choose n}}.}
この確率は普通の仮説検定で有意差を表す「p値」とは違い、p値を求めるには（普通の検定と同じように）実際の観測データよりも極端な場合も含めて考えなければならない。また、成功/失敗を検討してはいるが、ビー玉を取り出す毎に壺の中に残されたビー玉の個数は次々に変化し、各試行での成功確率は同じではないため、この問題は二項分布 では正確にモデル化できない。
四分割表に対する独立性の検定 との対比を取るために、この問題を四分割表で表現することを考える。N,m,nが固定されれば周辺度数（marginal frequency：第3列および第3行の値）は全て固定され、下表のようになる。さらに、O11を確定すれば、残りのO12,O21,O12は確定する。今、ここで、さらに、O11=X=kとすると、下表のように、四分割表の値が全て確定する。
緑玉(成功) 赤玉（失敗） Row Total
壺から取り出された
O11=k
O12=n − k
n
壺に残った
O21=K − k
O22=N + k − n − K
N − n
Column Total K N − K N
このとき、例えば, k=4であれば、四分割表とP(X=4)は以下のようになる。
P
(
X
=
4
)
=
f
(
4
;
50
,
5
,
10
)
=
(
5
4
)
(
45
6
)
(
50
10
)
=
5
⋅
8145060
10272278170
=
0.003964583
…
.
{\displaystyle P(X=4)=f(4;50,5,10)={{{5 \choose 4}{{45} \choose {6}}} \over {50 \choose 10}}={5\cdot 8145060 \over 10272278170}=0.003964583\dots .}
緑玉(成功) 赤玉（失敗） Row Total
壺から取り出された
4
6
10
壺に残った
1
39
40
Column Total 5
45
50
さらに、k=5の場合を考える。P(X=5)は以下のようになる。
P
(
X
=
5
)
=
f
(
5
;
50
,
5
,
10
)
=
(
5
5
)
(
45
5
)
(
50
10
)
=
1
⋅
1221759
10272278170
=
0.0001189375
…
,
{\displaystyle P(X=5)=f(5;50,5,10)={{{5 \choose 5}{{45} \choose {5}}} \over {50 \choose 10}}={1\cdot 1221759 \over 10272278170}=0.0001189375\dots ,}
これらを比較すると、緑玉が5個の取り出される確率は、4個取り出される確率より約35倍低くなることが判る。
超幾何分布と幾何分布 は名前の上で類似しているが、分布としては全くの別物だと考えてよい。それぞれの名前は確率関数から生まれる列 が超幾何数列 、幾何数列 であることに由来する。
^ 二項分布は超幾何分布の定義における「非復元抽出」を「復元抽出」に置き換えたものに相当する。
蓑谷千凰彦、統計分布ハンドブック、朝倉書店 (2003).
B. S. Everitt（清水良一訳）、統計科学辞典, 朝倉書店 (2002).
M. Galassi et al.（富永大介訳）、GNU Scientific Library リファレンスマニュアル ver. 1.8, p. 199 (2006).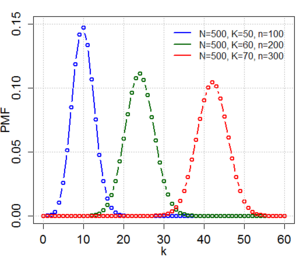 
![{\displaystyle 1-{\frac {{\binom {n}{k+1}}{\binom {N-n}{K-k-1}}}{\binom {N}{K}}}\,{}_{3}\!F_{2}\!\!\left[{\begin{array}{c}1,\ k+1-K,\ k+1-n\\k+2,\ N+k+2-K-n\end{array}};1\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9736814225d82071d71d86813542aebf591aa1e3)
![{\displaystyle {\frac {(N-2K)(N-1)^{\frac {1}{2}}(N-2n)}{[nK(N-K)(N-n)]^{\frac {1}{2}}(N-2)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9ec1b0c28225251fa3fd794e30bffc3eb34315e)
![{\displaystyle 6nK(N-K)(N-n)(5N-6){\Big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/961bbad35da7cd59eb05fb969e0f817f9b1e254c)
![{\displaystyle E[X_{i}]={\frac {nK_{i}}{N}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc387f25386ce576b99ffba6b2db8b2f630e289a)
![{\displaystyle \operatorname {Var} [X_{i}]={\frac {(N-n)n(N-K_{i})K_{i}}{(N-1)N^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5a227cae18f463bc62df52414be37edded71d07)
![{\displaystyle \operatorname {Cov} [X_{i},X_{j}]=-{\frac {(N-n)nK_{i}K_{j}}{(N-1)N^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9dcfaad3486640b44b5c9c51a171eea0fddea43b)
