自己準同型
数学における自己準同型(じこじゅんどうけい、英: endomorphism)とは、ある数学的対象からそれ自身への射(あるいは準同型)のことを言う。例えば、あるベクトル空間 V の自己準同型は、線型写像 ƒ: V → V であり、ある群 G の自己準同型は、群準同型 ƒ: G → G である。一般に、任意の圏に対して自己準同型を議論することが可能である。集合の圏において、自己準同型はある集合 S からそれ自身への函数である。
任意の圏において、X の任意の二つの自己準同型写像の合成は再び X の自己準同型である。X のすべての自己準同型の集合はモノイドを構成し、それは End(X) と表記される(あるいは、圏 C を強調するために EndC(X) と表記される)。
自己同型
編集X の可逆な自己準同型は、自己同型と呼ばれる。すべての自己同型の集合は、群構造を備える End(X) の部分集合であり、X の自己同型群と呼ばれ、Aut(X) と表記される。次の図で、矢印は包含関係を表す:
| 自己同型 | 同型 | |
| 自己準同型 | 準同型 |
自己準同型環
編集あるアーベル群 A の自己準同型写像は、次のルールに従って足し合わされる:(ƒ + g)(a) = ƒ(a) + g(a)。この加法の下で、アーベル群の自己準同型写像は環(自己準同型環)を構成する。例えば、Zn の自己準同型写像の集合は、成分が整数であるような全ての n × n 行列からなる環である。ベクトル空間あるいは環上の加群の自己準同型写像もまた、前加法圏内の任意の対象の自己準同型写像と同様に、環を構成する。非アーベル群の自己準同型写像は、近環として知られる代数的構造を生成する。乗法単位元をもつすべての環は、その正則加群の自己準同型環であり、したがってあるアーベル群の自己準同型環の部分環である[1]。しかし、どんなアーベル群の自己準同型環でもないような環も存在する。
作用素論
編集特にベクトル空間のような任意の具象圏において、自己準同型はある集合からそれ自身への写像であり、その集合上の単項演算子として解釈されることもある。それは元に対して作用し、元の軌道の概念の定義を許すものである。
手近な圏に対して定義される追加構造(トポロジー、距離など)に依存して、そのような作用素は連続性や有界性などの性質を持つこともある。その点に関する詳細は作用素論に関係する記事を参照されたい。
自己函数
編集自己函数(英: endofunction)とは、その定義域が余域と等しい函数のことを言う。準同型な自己函数は、自己準同型である。
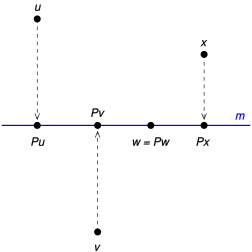
S を任意の集合とする。S 上の自己函数の中に、S と、各 に関連する与えられた定数 の置換が存在する。S のすべての置換は、その定義域と等しい余域を持ち、それは可逆な双射である。S が 1 より多い元を持つなら、S 上の定数函数は、その定義域の真部分集合であるような余域を持ち、双射ではない(また可逆でもない)。各自然数 n に対する n/2 の床函数に対応する函数は、余域と定義が等しいが、可逆ではない。
有限の自己函数は、有向擬森と等しい。大きさ n の集合に対し、その集合上には nn 個の自己函数が存在する。
特定の双射自己函数は、対合、すなわちその逆と一致する函数である。
関連項目
編集注釈
編集- ^ Jacobson (2009), p. 162, Theorem 3.2.
参考文献
編集- Jacobson, Nathan (2009), Basic algebra, 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1
外部リンク
編集- Hazewinkel, Michiel, ed. (2001), “Endomorphism”, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Endomorphism - PlanetMath.org