垂足円
垂足円(すいそくえん、英: pedal circle)は、幾何学において三角形ABCと点Pについて決まる特別な円である。具体的には、点Pから△ABCの辺に降ろした垂線と辺の交点Pa, Pb, Pc(垂足)が成す三角形(垂足三角形)の外接円を指す用語[1][2]。
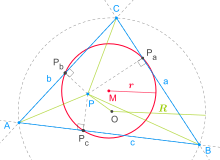
Pの各辺における垂足Pa, Pb, Pc。
外心O。
緑の線はPの垂足円半径を表すのに使われる線分。

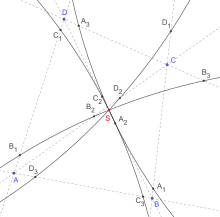
垂足円は6つの垂足Pa, Pb, Pc、Qa, Qb, Qc。
垂足円の中心Mは線分PQの中点。
角の二等分線wa, wb, wc。
基準三角形の外心をO、外接円の半径をRとして、Pの垂足円の半径rPは次の式で表される[2]。
Pが基準三角形の外接円上にあるとき、この式の分母は0になる。これはPの垂足三角形が退化してシムソン線となり、その垂足円は半径が無限大の円となるためである。Pが基準三角形の内心であるとき、その垂足円は基準三角形の内接円である。Pが基準三角形の垂心または外心であるとき、その垂足円は九点円である[3]。
Pを外接円上にない点として、Pの等角共役点Qの垂足円はPの垂足円と一致する。つまり垂足Pa, Pb, PcとQa, Qb, Qcは同一円周上にある。さらに垂足円の中心は線分PQの中点である[1]。
一般化
編集2021年斎藤輝は、対垂三角形を対等角三角形に一般化するように、垂足円を任意の角に一般化した[5]。
- 等角共役点P, Qをそれぞれ各辺にθ, -θの角度で射影した点、延べ6点は共円である。
θ = 90°とすれば垂足円を得る。
出典
編集- ^ a b Ross Honsberger: Episodes in Nineteenth and Twentieth Century Euclidean Geometry. MAA, 1995, pp. 67–75
- ^ a b Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007 (reprint), ISBN 978-0-486-46237-0, pp. 135–144, 155, 240
- ^ a b Weisstein, Eric W. "Pedal Circle". mathworld.wolfram.com (英語).
- ^ Weisstein, Eric W. "Griffiths' Theorem". mathworld.wolfram.com (英語).
- ^ 齋藤輝 (2021). “シムソン線,9点円の一般化とオイラー・ポンスレ点”. 塩野直道記念 第9回「算数・数学の自由研究」作品コンクール.
関連項目
編集外部リンク
編集- ウィキメディア・コモンズには、垂足円に関するカテゴリがあります。
- Pedal Circle of Isogonal Conjugates - GeoGebra
- pedal triangle and pedal circle
- 等角共役点


