ランプ関数(英: ramp function)とは、一変数の実関数であり、独立変数とその絶対値の平均として容易に求められる。区分線形関数。
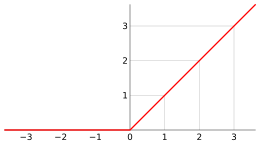 ランプ関数のグラフ
ランプ関数のグラフ
この関数は工学において(DSPの理論など)応用を持つ。"ramp function"の名は、グラフの形状が傾斜路(英: ramp)に似ていることに由来する。
ランプ関数は定義域全体で非負となる。
-
そのため、関数の値はその絶対値に等しい。
-
ランプ関数の導関数はヘビサイド関数に等しい。
-
ランプ関数は次の微分方程式を満たす。但し δ(x) はディラックのデルタ関数である。
-
これは、R(x) が二階微分作用素のグリーン関数であることを意味する。これにより、可積分な二階導関数 f′′(x) を持つ任意の関数 f(x) は、a < x < b のとき次の方程式を満たす。
-
ランプ関数のフーリエ変換は次の通りとなる。
-
ここで δ(x) は ディラックのデルタ関数(式中では導関数が使用されていることに注意)。
ランプ関数の片側ラプラス変換は次の通りとなる。
-
ランプ関数の任意の反復合成はランプ関数に等しい。[2]
-
- ^
これは max(a,b) が次のように定義できることによる。
-
これを最大値関数による定義 R(x) := max(x,0) に代入すればよい。
- ^
次の証明には非負性が用いられている。
-
