g = 1; l = 1; \[Alpha] = 0.05; v0 = 2.5;
sol = NDSolveValue[{\[Theta]''[t] + \[Alpha] \[Theta]'[t] + g/l Sin[\[Theta][t]] == 0, \[Theta][0] == 0, \[Theta]'[0] == v0}, \[Theta], {t, 0, 200}];
f[t_] := Evaluate[{Mod[sol[t], 2 \[Pi], -\[Pi]], D[sol[t], t] }];
frames = Table[
Grid[{{
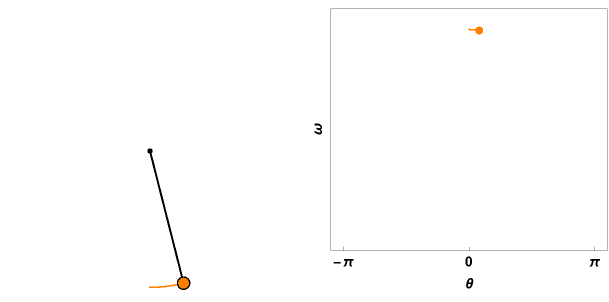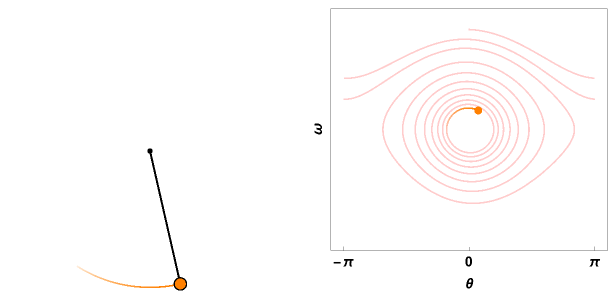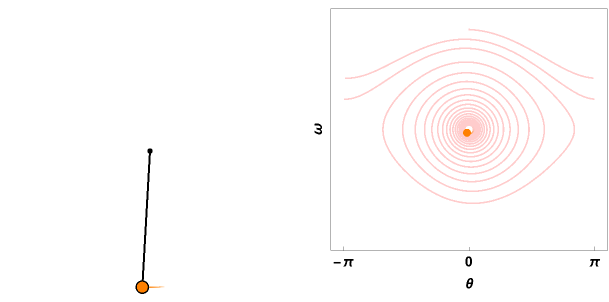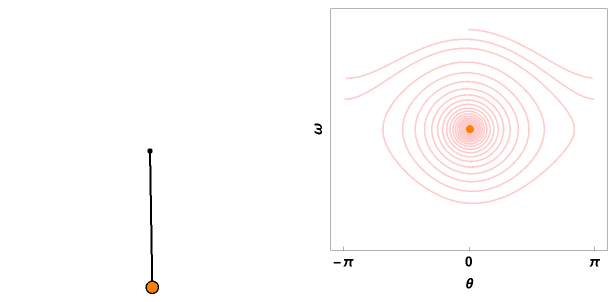
ParametricPlot[ Evaluate[{Sin[sol[t]], -Cos[sol[t] ]}], {t, 0, \[Tau]}, PlotRange -> 1.1 {{-l, l}, {-l, l}}, ColorFunction -> Function[{x, y, u}, RGBColor[1, 1 - (E^(-((u - 1)^2/(2 (1/\[Tau])^2))))/2,
1 - E^(-((u - 1)^2/(2 (1/\[Tau])^2)))] ], Axes -> False, Epilog -> {Black, Thick, Disk[{0, 0}, 0.02], Line[{{0, 0}, Evaluate[{Sin[sol[\[Tau]]], -Cos[sol[\[Tau]]]}]}], Disk[Evaluate[{Sin[sol[\[Tau]]], -Cos[sol[\[Tau]]]}, 0.05]], Orange, Disk[Evaluate[{Sin[sol[\[Tau]]], -Cos[sol[\[Tau]]]}, 0.04]]}, ImageSize -> 300]
,
ParametricPlot[f[t], {t, 0, \[Tau]}, PlotRange -> 1.1 {{-\[Pi], \[Pi]}, 1.1*{-v0, v0}}, PerformanceGoal -> "Quality", ColorFunction -> Function[{x, y, u}, RGBColor[1, 0.8 - (0.8 - 0.5) (E^(-((u - 1)^2/(2 (1/\[Tau])^2)))), 0.8 (1 - E^(-((u - 1)^2/(2 (1/\[Tau])^2))))] ], FrameLabel -> {"\[Theta]", "\[Omega]"}, LabelStyle -> {Black, Bold, FontSize -> 14}, FrameTicks -> {{None, None}, {{-\[Pi], 0, \[Pi]}, None}},
Epilog -> {Orange, Disk[f[\[Tau]], 0.1]}, Axes -> False, Frame -> True, ImageSize -> 300]
}}]
, {\[Tau], 0.1, 200, 0.5}];
ListAnimate[frames]