ネットワーク理論
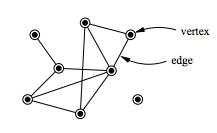
ネットワーク理論(ネットワークりろん)は、通信、コンピュータ、生物、ソーシャルなどの複雑ネットワークを研究する分野。ネットワークは、ノードやエッジが属性(例:名前)を持つグラフとして定義される。数学のグラフ理論、物理学の統計力学、コンピュータサイエンスのデータマイニングと情報視覚化、統計からの推論モデリング、社会学の社会構造などの理論や手法が使われる[1]。
概論・歴史
編集ネットワーク理論は、複雑なデータを解析する手段としてさまざまな分野で言及される。この理論の最初期の論文は、1736年にレオンハルト・オイラーによって書かれた有名な「七つの橋」の問題である。オイラーの頂点と辺による数学的証明はグラフ理論の基礎となった。グラフ理論は発展して化学に応用された[2]。
1930年代、伝統的なゲシュタルト派の心理学者ヤコブ・モレノはアメリカで社会学を発展させ、1933年4月にソシオグラムを医療学者の会で発表した。モレノは「ソシオグラムの出現以前はあるグループでの対人関係の構造が正確にどのようなものか、誰も分かりませんでした。」と発表した[3]。ソシオグラムの例が左の図で、小学1年生の社会的構造の表象である。男子と女子はそれぞれ同性が友達だったが、例外の1人の男子が女子を好きだと言ったが、相互的な関係ではないことが分かる(図を参照)。ソシオグラムは多くの用途を見出しており、社会ネットワーク解析という分野に発展している。
ネットワーク理論における確率論は、ポール・エルドシュとアルフレッド・レニーのランダムグラフに関する8つの有名なグラフ理論の論文から派生した。社会的ネットワークの場合は指数ランダムグラフのモデル(p*)がネットワークで発生する関係の確率空間を表すために使われる。ネットワーク確率論に対する別のアプローチは確率マトリックスである。確率マトリックスは、ネットワークのサンプルに見られるエッジの過去の有無に基づいて、ネットワーク全体に発生するエッジの確率をモデルにする。
1998年にデイビッド・クラックハートとキャサリン・カーリーは、PCANSモデルを用いたメタネットワークの概念を発表し、すべての組織は3つのドメイン:個人・タスク・リソースから構成されるとした。該当の論文によると、ネットワークは複数のドメインにまたがって発生し、相互に関連する。この分野は、ダイナミックネットワーク解析と呼ばれる分野に発展した。
最近の動向としては、ネットワーク理論を使って位相幾何学を数学的に表す取り組みが注目を浴びている。ダンカン・ワッツは、数学的表現を持つネットワーク上で実験データを使ってスモールワールド現象を発表した。バラバーシ・アルベルト・ラースローとレカ・アルベルトは、スケールフリーのネットワークを実現させた。これは多数の接続を持つハブ頂点を含む広義のネットワークトポロジーであり、他のすべてのノードと接続の数の比率が一定に保たれるように成長する。インターネットなどの多くのネットワークはこの側面を維持しているように見えるが、他のネットワークではこの比率はノードの長いテール分布に近似する。
プロパティ
編集多くのネットワークには、その特性の解析に使われる性質がある。 これらの特性(プロパティ)は多くの場合、ネットワークモデルを定義することで特定のモデルとの対比の解析に使われる。 ネットワーク科学で使われる用語の定義の多くは、グラフ理論でも使われる。
密度
編集無向ネットワークの密度 は、辺の数 と、二項係数 によって得られる可能な辺の数の比として定義される:
ネットワークが有向である場合、可能な辺の数は となるため、密度は次のように定義される:
大きさ
編集ネットワークの大きさは、ノード の数か、もしくは(一般的ではないが)エッジ の数で表す。エッジ の数は (木) から (完全グラフ)までさまざまである。
平均次数
編集ノードの次数 とは、そのノードに接続している辺の数である。 ネットワークの密度にも密接に関連する平均次数は、 である。 ERランダムグラフモデルでは、 を計算できる。ここでは、 は2つのノードが繋がっている確率である。
平均距離
編集平均距離(Average path length)は、すべてのノードのペア間の最短距離を見つけて加算し、ペアの総数で割ることで算出される。 これは、ネットワークのあるノードから別のノードに到達するまでの平均のステップの数を表している。
直径
編集ネットワークを測定する別の手段として直径が使われる。ネットワークの直径は、ネットワーク内の最短距離のうち最も長いものとして定義される。 これは、ネットワーク内の最も離れた2つのノード間の最短距離となる。 言い換えれば、各ノードから他のすべてのノードまでの最短距離を計算すると、直径はすべての距離のうち最も長いものとなる。 直径は、ネットワークの線形的な大きさを表す。
クラスター係数
編集クラスター係数とは、「all-my-friends-know-each-other(すべての友達が互いを知っている)」特性を表す。 「友人の友人は友人である」とも表現される。 ノードのクラスター係数とは、ノードが近隣のノードと互いに実際に存在しているリンクと、可能なリンクの最大数の比率である。 ネットワーク全体でのクラスタ係数は、全ノードのクラスター係数の平均である。 ネットワークのクラスター係数が高いことは、スモール・ワールドであることの指標でもある。 番目のノードのクラスター係数は と表される。ここでは、 は 番目のノードの隣人の数であり、 はこれらの隣人間のリンクの数である。 隣人間の可能なリンクの最大数は以下のように表される:
連結性
編集ネットワークがどのように連結されているか、すなわちノードの間にエッジを伝う道があるかは、ネットワークやその部分グラフの重要な特徴の一つである。連結性に応じて、以下のようなネットワークや部分グラフの種類がある。
- 完全グラフ・クリーク:すべてのノードが他のすべてのノードとリンクで直接つながっているネットワークを完全グラフといい、ネットワークに含まれる、完全グラフをなす部分グラフをクリークという。
- 巨大連結成分:ネットワークの一定割合を占める連結成分。厳密には、大きさがネットワーク全体の大きさに比例する連結成分を指す。ランダムグラフでは巨大連結成分が高々1つしか存在しないことが知られている。
- 弱連結成分:有向ネットワークで、エッジの方向を無視した場合、どのノードからも他のノードへの道が存在する連結成分。
- 強連結成分:有向ネットワークで、エッジの方向を考慮した場合、どのノードからも他のノードへの道が存在する連結成分。
ノードの中心性
編集中心性の指数は、ネットワークモデルにおいて最も重要なノードを特定するために使われる。中心性の指数で割り出される「重要度」とはネットワークによって意味が異なる。 例えば、中間中心性では、他の多くのノード間にブリッジを形成するノードを非常に重要とみなす。また、固有値の中心性は、他の多くの重要なノードがそれにリンクしている場合に重要とみなされる。 このように重要度の定義は数多くの文献で言及されている。中心性指数は、最も重要なノードを識別するためにのみ適用が可能であり、他のノード部分では無意味な場合がほとんどである[4][5][6]。例えば、2つの別々のコミュニティがあり、互いとのリンクはそれぞれの最も若いメンバー同士にしかないとする。すると、 1つのコミュニティからもう1つのコミュニティへの移行するには必ずこのリンクを経由しなければならないので、2人の若いメンバーは高い中間中心性を持つことになる。 しかし、彼らは若いため、おそらくコミュニティ内の重要ノードとはリンクが少なく、固有値の中心性は非常に低い。静的ネットワークの文脈における中心性の概念は、経験的および理論的研究に基づいて、時間的ネットワークの文脈におけるダイナミック中心性[7]に拡張されている[8][9]。
ノードの影響
編集中心性指数の欠点を克服するため、より一般的な尺度として開発されたのが、アクセシビリティ(ネットワークの残りの部分があるノードからどの程度アクセスが可能であるかを測定するために、ランダムウォークの多様性を使用する)[10]と、影響力(ノードの感染力の期待値から割り出される)である。これらの測定値は、ネットワークの構造のみから計算することができる[5]。
モデル
編集ネットワークモデルは、複雑ネットワーク内に起こる相互作用の理解に役立つ。また、ランダムグラフから生成されたネットワーク構造のモデルは実際の複雑ネットワークと見比べられて使われる。
Erdős-Rényi(ER)
編集Paul ErdősとAlfréd Rényiの名前にちなんだErdős-Rényiモデルは、エッジが等しい確率のノード間に設定されたランダムグラフを生成する。 確率方法で、さまざまなプロパティを満たすグラフの存在を証明したり、多くのグラフに対してあるプロパティが持つ重要性を厳密に定義したりできる。Erdős-Rényiモデルを生成するには2つのパラメータが必要である。1つは、生成されたグラフ内のノード数 N と、ある2つのノード間でリンク p を形成する確率である。E をエッジ数の期待値とすると、 式 ⟨k⟩ = 2 ⋅ E / N = p ⋅ (N − 1) を使って定数 ⟨k⟩ を導き出せる。
Erdős-Rényiモデルには、他のグラフと比べるといくつかの興味深い特徴がある。 このモデルは特定のノードにバイアスをかけずに生成されるため、次数分布は次の式のように二項式となる:
また平均次数⟨k⟩が一定で、ノード数 N が増えるにつれ、クラスター係数が0へと小さくなる。 このモデルでは ⟨k⟩ > 1 において、巨大連結成分が存在する(この現象を「パーコレーション」と呼ぶ)。 またこのモデルでは、平均距離が比較的短く、log N に近くなる。
ワッツ・ストロガッツ
編集ワッツ・ストロガッツのランダムグラフモデルは、スモール・ワールド特性を持つグラフを生成するモデルである。このモデルを生成するためにはまず格子構造が必要である。ネットワークの各ノードは、当初は、その 隣のノードにリンクされている。もう1つのパラメータとして、再配線確率が必要である。各エッジは確率 でランダムエッジとして再配線される。このモデルで再配線されるリンクの期待値は である。
このモデルは、最初は非ランダムの格子構造なので、平均距離が高いとともにクラスター係数が非常に高い。再配線の確率が上がるにつれて、クラスター係数は平均距離よりも遅く減少する。この特徴はクラスター係数の減少を抑えながら、ネットワークの平均距離が大幅に減少することを可能にする。確率 の値が高いほど、多くのエッジが再配線され、ワッツ・ストロガッツモデルは実質的にランダムなネットワークになる。
バラバシ・アルバート(BA)
編集BAモデルは、優先的アタッチメント(preferential attachment)または「富裕層がより豊かになる」現象を実証できるランダムネットワークモデル。 このモデルでは、エッジはそれより高い度合いのノードに接続する可能性が高い。ネットワークは最初はm0 個のノードを持ち、m0 ≥ 2でネットワークの各ノードの次数は 1以上でなければならない。そうでないと、ネットワークの残りの部分から常に孤立した状態になる。
BAモデルでは、新しいノードが1つずつネットワークに追加される。 各新しいノードは、既存のノードが既に持つリンクの数に比例する確率で、既存のノード 個にリンクされる。 まとめると、新しいノードがあるノード に接続される確率 は以下のようになる[11]。 はノード の次数である。
ここで、重リンクされたノード(ハブと呼ばれる)は、さらに多くのリンクを蓄積する傾向にあるが、少数のリンクしか持たないノードは新しいリンクの宛先として選択される可能性は低い。 つまり、新しいノードには、すでに多くリンクされたノードにリンクする傾向にある。
BAモデルから得られる次数分布はスケールフリーであり、べき乗則で表される:
ハブとなる重リンクされたノードは、ノード間の短い道(Path)の存在を可能にする、高い中間中心性を示す。 結果として、BAモデルは平均距離が非常に短くなる傾向にある。 このモデルのクラスター係数も0になる傾向がある。Erdős Rényiモデルや、スモールワールド・ネットワークを含む多くのモデルの直径Dはlog Nに比例するが、BAモデルはD〜loglogNとなる。このときの平均距離はNを直径としたときの縮尺であることに注意。
仲介駆動型接続(MDA)
編集Mediation-Driven Attachment(MDA、仲介駆動型接続)モデルでは、 個のエッジを持つ新しいノードが既にリンクされているノードをランダムに選択し、そのノードだけでなく、その隣人のノード 個にランダムにリンクする。 既存のノード が新しいノードに選ばれる確率 は以下のようになる:
この式の2つ目の因数は、調和平均(IHM)の逆数である。ノード の 近傍の次数(IHM)を計算する。 大規模な数値の研究によると、 の場合、大きな限度 における調和平均は定数となり、これは と表せられる。これは、ノードが持っているリンク(度数)が高いほど、より多くのリンクが得られる傾向を意味し、「富裕層がより豊かになる」現象を説明する。したがって、MDAネットワークはPAの法則に密かに従っている[12]。
の場合、「1人がすべてを手に入れる」メカニズムが見られる。ここでは、ノードのほぼ が次数1を持ち、1人が超富裕層となる。「富裕層がより豊かになる」現象は、 から見られる。
フィットネス
編集Caldarelliらによって導入されたフィットネスモデルでは、頂点の性質が重視される[13]。このモデルでは、2つの頂点 の間のリンクが関数 によって算出される確率を持つ。頂点 の度数は以下のように表せる[14]:
が に逆数を持ち、かつ増加する関数である場合、確率分布 は以下のようになる:
結果として、 がべき乗則として分配される場合、ノード次数も同様になる。速い崩壊確率分布ではリンク関数と共に、 と となる。
ヘヴィサイド関数の 定数と を使用すると、スケールフリーのネットワークとなる。
このモデルは、さまざまなノード に対するフィットネスにGDPを使用することによって、国家間の貿易を記述することに成功している[15][16]:
解析
編集この節の加筆が望まれています。 |
コンテンツ普及
編集この節の加筆が望まれています。 |
相互ネットワーク
編集この節の加筆が望まれています。 |
多層ネットワーク
編集この節の加筆が望まれています。 |
ネットワーク最適化
編集この節の加筆が望まれています。 |
関連項目
編集脚注
編集- ^ Committee on Network Science for Future Army Applications (2006). Network Science. National Research Council. ISBN 0309653886.
- ^ シルベスター、1878
- ^ モレノ、1953
- ^ Lawyer, Glenn (March 2015). "Understanding the spreading power of all nodes in a network". Scientific Reports. 5 (O8665): 8665. Bibcode:2015NatSR...5E8665L. doi:10.1038/srep08665. PMC 4345333. PMID 25727453.
- ^ a b Lawyer, Glenn (March 2015). "Understanding the spreading power of all nodes in a network". Scientific Reports. 5 (O8665): 8665. Bibcode:2015NatSR...5E8665L. doi:10.1038/srep08665. PMC 4345333. PMID 25727453.
- ^ Borgatti, Stephen P. (2005). "Centrality and Network Flow". Social Networks. Elsevier. 27: 55–71. doi:10.1016/j.socnet.2004.11.008.
- ^ Braha, D.; Bar-Yam, Y. (2006). "From Centrality to Temporary Fame: Dynamic Centrality in Complex Networks". Complexity. 12: 59–63. doi:10.1002/cplx.20156.
- ^ Hill, S.A.; Braha, D. (2010). "Dynamic Model of Time-Dependent Complex Networks". Physical Review E. 82: 046105. doi:10.1103/physreve.82.046105.
- ^ Holme, P. and Saramäki, J. 2013. Temporal Networks. Springer.
- ^ Travençolo, B. A. N.; da F. Costa, L. (2008). "Accessibility in complex networks". Physics Letters A. 373 (1): 89–95. Bibcode:2008PhLA..373...89T. doi:10.1016/j.physleta.2008.10.069.
- ^ R. Albert; A.-L. Barabási (2002). "Statistical mechanics of complex networks" (PDF). Reviews of Modern Physics. 74: 47–97. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. doi:10.1103/RevModPhys.74.47.
- ^ Hassan, M. K.; Islam, Liana; Arefinul Haque, Syed (2017;). "Degree distribution, rank-size distribution, and leadership persistence in mediation-driven attachment networks". Physica A. 469: 23–30. doi:10.1016/j.physa.2016.11.001
- ^ Caldarelli G., A. Capocci, P. De Los Rios, M.A. Muñoz, Physical Review Letters 89, 258702 (2002)
- ^ Servedio V.D.P., G. Caldarelli, P. Buttà, Physical Review E 70, 056126 (2004)
- ^ Garlaschelli D., M I Loffredo Physical Review Letters 93, 188701 (2004)
- ^ Cimini G., T. Squartini, D. Garlaschelli and A. Gabrielli, Scientific Reports 5, 15758 (2015)
参考文献
編集この節の加筆が望まれています。 |