シフラー点
平面幾何学における三角形のシフラー点（シフラーてん・英語: Schiffler point）は、任意の三角形から一意的に定義できる点である[1][2][3][4]。名称は1985年にこの点を定義したKurt Schiffler(en)に由来する。
定義
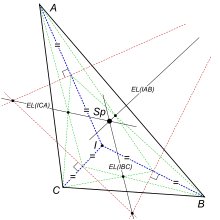
編集三角形ABCの内心を I とする。3つの三角形 IAB,IBC,ICA のオイラー線は ABC のオイラー線上の一点で交わる。この交点をシフラー点とする。
証明
編集3本のオイラー線が1点で交わることは以下のように証明できる[5]。
三角形 ABC の内心を I、外心を O、垂心を H とする。三角形 IBC の外心を O'、垂心をH' とし、O'H' が OH と交わる点を P、AH と交わる点を A' とする。ABC の外接円の半径を R とする。
O' は ABC の外接円の弧BC の中点である。よって OO'=R。BC の中点を M とすると、2MO'=IH'。IH' と AH は平行なので IH':AA'=O'I:O'A。これらを整理すると HA'=AH+BH+CH となる。
OP:PH=OO':HA' は、A,B,C の取り方によらず一定である。よって3本のオイラー線は1点で交わる。
座標
編集三角形の3辺の長さを a, b, c としたとき、シフラー点の三線座標は以下のようになる。
![{\displaystyle \left[{\frac {1}{\cos B+\cos C}},{\frac {1}{\cos C+\cos A}},{\frac {1}{\cos A+\cos B}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a071726d8d6eb07f6999925c9a31adef883d0ff5)
![{\displaystyle \left[{\frac {b+c-a}{b+c}},{\frac {c+a-b}{c+a}},{\frac {a+b-c}{a+b}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d29f47bdd36391d023c98ac9e124f845ff739f6)
重心座標では以下のとおりである。
![{\displaystyle \left[{\frac {a}{\cos B+\cos C}},{\frac {b}{\cos C+\cos A}},{\frac {c}{\cos A+\cos B}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16ae2e53216d368e02b1bf2d332ebe01929c2bdd)
![{\displaystyle \left[{\frac {a(b+c-a)}{b+c}},{\frac {b(c+a-b)}{c+a}},{\frac {c(a+b-c)}{a+b}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/240d62c66df5eebe33522b674c02a09edd8800b0)
歴史
編集Kurt Schiffler は、1985年にカナダの雑誌 Crux Mathematicorum(en)に問題を発表した。1986年に2人のオランダの数学者 G.R.Veldkamp と W.A.van der Spek によって証明が与えられている。この証明の掲載時にこの点を「シフラー点」と命名している。
4本のオイラー線が1点に交わる条件はこの問題が発表されるより50年以上前に研究されており、フランク・モーリーと Frank Vigor Morley によって「点P が外接円上かノイベルグ三次曲線上にある場合に4本のオイラー線が1点で交わる」と結論付けられている[6]。
脚注
編集- ^ Lev Emelyanov,Tatiana Emelyanova (2003). “A Note on the Schiffler Point”. Forum Geometricorum (Volume 3): 113–116.
- ^ Charles Thas (2004). “On the Schiffler center”. Forum Geometricorum (Volume 4): 85-95.
- ^ Antreas P. Hatzipolakis, Floor van Lamoen, Barry Wolk, Paul Yiu (2001). “Concurrency of Four Euler Line”. Forum Geometricorum (Volume 1): 59–68.
- ^ Khoa Lu Nguyen (2005). “Onthe Complement of the Schiffler Point”. Forum Geometricorum (Volume 5): 149–164.
- ^ 『幾何学大辞典』補巻2 P.51
- ^ Weisstein, Eric W. "Neuberg Cubic". mathworld.wolfram.com (英語).
参考文献
編集- Schiffler, Kurt (1985). “Problem 1018”. Crux Mathematicorum 11: 51.
- Veldkamp, G. R. & van der Spek, W. A. (1986). “Solution to Problem 1018”. Crux Mathematicorum 12: 150–152.
- 岩田至康『幾何学大辞典』補巻2 ISBN 4837506119
外部リンク
編集- Weisstein, Eric W. "Schiffler Point". mathworld.wolfram.com (英語).