オートマトン

オートマトン (単数形: 英: automaton [ɔːˈtɑməˌtɑn], 複数形: オートマタ（automata [ɔːˈtɑmətə]）) とは、自動人形などとも呼ばれる「オートマタ」と同じ語であるが、計算理論において、計算モデルに関して有限オートマトンなどの総称として使われる。また特に「オートマトン理論」と呼ばれる分野では、計算機械のうち計算可能性の点でチューリングマシンよりも制限されているものを特に指して言うこともある。

オートマトン理論

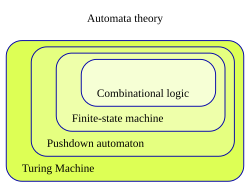
種類

• 有限オートマトン
  • 決定的有限オートマトン (Deterministic Finite Automaton, DFA)
  • 非決定的有限オートマトン (Nondeterministic Finite Automaton, NFA)
  • ε動作を含む非決定的有限オートマトン (Nondeterministic Finite Automaton, with ε transitions (FND-ε,ε-NFA))
• プッシュダウン・オートマトン (Pushdown Automaton, PDA)
• 線形拘束オートマトン (Linear Bounded Automaton, LBA)
• 生け垣オートマトン (Hedge Automata)

広義のオートマトン

• チューリングマシン (Turing Machine)
  • 決定的チューリングマシン (Deterministic Turing Machine, DTM)
  • 非決定的チューリングマシン (Nondeterministic Turing Machine, NTM)

形式言語の階層とオートマトン

→詳細は「形式言語の階層」を参照

→「チョムスキー階層」も参照

何らかの言語（特に形式言語）の文法（形式文法）と、それを生成する生成規則と、それを受理するオートマトンの間には対応関係があり、また言語を（形式言語を）集合とした場合に部分集合になっているという関係が階層をなしている、という事実がある。詳細は形式言語の階層の記事およびチョムスキー階層の記事を参照。

参考文献

• 米田政明 他 『オートマトン・言語理論の基礎』、 近代科学社、2003年、ISBN 4-7649-0297-4
• 岩間 一雄：「オートマトン・言語と計算理論」、コロナ社、ISBN 978-4339018219（2003年10月）。
• 藤原暁宏：「はじめて学ぶ　オートマトンと言語理論」、森北出版、ISBN 978-4-627-85291-4 (2015年7月21日)。
• Zvi Kohavi; Niraj K. Jha (2009), Switching and Finite Automata Theory (3rd ed.), Cambridge University Press, ISBN 0521857481, ISBN 9780521857482 

関連項目

• 抽象機械
• セル・オートマトン
• 状態機械
• 正規表現
• 形式文法