アンの定理
アンの定理(アンのていり、Anne's theorem)とは、四角形の面積に関する定理である。フランスの数学者ピエール=レオン・アン(Pierre-Léon Anne, 1806-1850)にちなんで命名された[1]。
定理
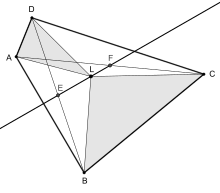
編集平行四辺形でない四角形ABCDの対角線の中点をE,Fとし、LをABCDの内部の任意の点とする。 LはABCDの辺を一つずつ持つ4つの三角形を形成する。 対向する三角形の面積の2つの合計が等しい(△BCL+△DAL=△LAB+△DLC)ならば、点Lはニュートン線上に位置する[2]。
平行四辺形の場合、対角線の中点が対角線の交点と一致するので、ニュートン線は存在しない。ただし、平行四辺形の任意の内部の点において、面積の同一性が成り立つ。
アンの定理の逆も成り立つ。つまり、四角形のニュートン線上の任意の点について、面積の同一性が成立する。
出典
編集- ^ Alsina, Claudi; Nelsen, Roger B. (2020-02-10) (英語). A Cornucopia of Quadrilaterals. American Mathematical Soc.. ISBN 978-1-4704-5312-1
- ^ Honsberger, Ross (1991) (英語). More Mathematical Morsels. Cambridge University Press. ISBN 978-0-88385-314-6
外部リンク
編集- Newton's and Léon Anne's Theorems - Cut the knot
- Weisstein, Eric W. "Léon Anne's Theorem". mathworld.wolfram.com (英語).
- Balanced areas in quadrilaterals – on the way to Anne’s Theorem
- Quadrilaterals