カウフマン多項式

結び目理論におけるカウフマン多項式（カウフマンたこうしき、英: Kauffman polynomial）は、ルイス・カウフマンに因む二変数結び目多項式である。カウフマン多項式はまず、絡み目図式に対して

$F(K)(a,z)=a^{-w(K)}L(K)$

と定められる。ただし w(K) はこの絡み目図式 K のひねり数で、K の L-多項式 L(K) は以下の性質によって絡み目図式上定義される二変数 a, z に関する多項式である:

• L(O) = 1 （O は自明な結び目）;
• L(s_r) = aL(s), L(s_ℓ) = a⁻¹L(s);
• L はライデマイスター II と III で不変である。

ここに、s は結び目の弦 (strand) で s_r および s_ℓ は、同じ弦 s にそれぞれ右手および左手ひねりを、ライデマイスター I を用いて加えたものとする。

さらに L はカウフマンのスケイン関係式:

カウフマン多項式のスケイン関係式

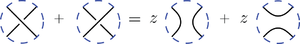
を満足しなければならない。上式において各項の図は、特定部分の円板の中だけが示された通り異なるが外側ではまったく一致するような絡み目図式たちの L-多項式 を表している。

カウフマンはこのような L が存在し、そのような L は無向絡み目の正則同位不変量であることを示した。ここから容易に F が有向絡み目の全同位不変量となることが従う。

ジョーンズ多項式はカウフマン多項式の、L-多項式としてブラケット多項式をとったときの、特別の場合である。カウフマン多項式は SO(N) に対するチャーン–シモンズのゲージ理論に関係する（ホンフリー多項式が SU(N) に対するチャーン–シモンズゲージ理論に関係するのと同じ仕方で）。

関連文献

• Kauffman, Louis (1987). On Knots. ISBN 0-691-08435-1 

外部リンク

• Hazewinkel, Michiel, ed. (2001), “Kauffman polynomial”, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Kauffman_polynomial 
• "The_Kauffman_Polynomial", The Knot Atlas.