Wikipedia

ウォルシュ・ダイアグラム

（ウォルシュダイアグラムから転送）

ウォルシュ・ダイアグラム（英: Walsh diagrams）は、ゆがみ座標（結合角）に対する計算された分子のオービタル結合エネルギーの表現である。小分子の幾何構造に関して素早く予測を行うために用いられる[1][2]。角座標図やウォルシュの相関図とも呼ばれる。幾何構造変化の関数として分子の分子軌道準位の変化をプロットすることによって、ウォルシュ・ダイアグラムは、なぜ分子がある空間的形状でより安定か（例えばなぜ水は曲がった配座をとるのか）を説明する[3]。

HAH分子のウォルシュ・ダイアグラム

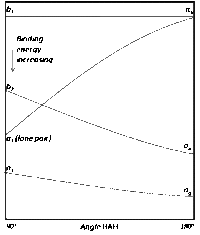
ウォルシュ・ダイアグラムの主な用途は、価電子の数が同一である関連分子で観察される構造の規則性を説明すること（例えば、なぜH2OとH2S似ているか）、電子の数やスピン状態の変化にしたがって分子の幾何構造がどのように変化するかを説明することである。加えて、ウォルシュ・ダイアグラムは、分子が幾何的摂動を受けた時にLUMO（最低空分子軌道）がどのようにHOMO（最高被占分子軌道）に影響するかという知識から分子の幾何構造の歪みを予測するために使うことができる。

分子の形状を予測するためのウォルシュの規則は、分子はそのHOMOに対して最もよい安定性を与える構造を取る、と述べる。もし特定の構造変化がHOMOに摂動を与えないならば、最も近い被占分子軌道が幾何的配向性に対する好みを左右する[4]。

歴史

編集

ウォルシュ・ダイアグラムは、ダンディー大学（英語版）の化学の教授であったA・D・ウォルシュ（英語版）によって、Journal of the Chemical Societyの一つの号に掲載された一連の10報の論文において初めて発表された[5][6][7][8][9][10][11][12][13][14]。ここで、ウォルシュはマリケンによる理論的貢献を適用することによって、基底状態と励起状態における多原子分子がとる形状を理論的に説明することを目標とした。具体的には、ウォルシュは、分子軌道のエネルギーに対する分子の形状の変化の影響を計算し、説明した。ウォルシュ・ダイアグラムはこのような依存性の説明図であり、ウォルシュの結論は「ウォルシュの規則」と呼ばれているものである[15]。

論文において、ウォルシュは複数の分子を例にとり、基底状態において分子がとる幾何構造は主に価電子の数に依存していることを示した[16]。ウォルシュ自身はこの一般概念が新しいものではないことを認めていたが、新しいデータによって以前の一般化を説明し磨きをかけられると説明した。ウォルシュはまた、マリケンは、2つの異なる核配置における多原子分子の可能なオービタルに対する相関図を構築しようと以前試み、基底状態と励起状態における分子の形状とスペクトルを説明するためにこの図を用いようと試みてさえもいた、とも記している[17][18]。しかしながら、マリケンは結合角が増大するにしたがってある曲線が上がったり下がったりする理由を説明することができなかったため、ウォルシュは彼の「ダイアグラムは実験に基づいたもので、未発表の計算に基づいたものである」と主張した[5]。

概要

編集

ウォルシュはそもそも、結合角に対して彼が「軌道結合エネルギー」と言い表すものをプロットすることによって相関図を構築した。ウォルシュがこの用語によって実際に言い表したものは不明である。ある者は、ウォルシュが実際はイオン化ポテンシャルを指していたと考えているが、これについてはまだ論争が続いている[19]。ともかく、ウォルシュが提示した一般概念は、分子の全エネルギーがその分子における全ての「軌道結合エネルギー」の和に等しい、というものであった。ゆえに、分子の結合角の変化による個々の軌道の安定化あるいは不安定化の知見から、分子の特定の状態に対する平衡結合角が予測できる。一つの配置（例えば直線状）を安定化するために相互作用する複数の軌道は、別の形状（例えば曲がった形状）においては重なり合うこともあれば合わないこともあり、したがって一つの幾何構造が計算的に別の構造よりも安定であるかが分かる。

典型的には、内殻軌道（B、C、N、O、F、Neに対する1s）は、エネルギー的に低く、結合角の変動によって大きく変化しないため、ウォルシュ・ダイアグラムから除かれる。原子価軌道のみが考慮される。しかしながら、原子価軌道の一部はしばしば占有されていないことを心に留めておくべきである。

ウォルシュ・ダイアグラムの生成

編集

ウォルシュ・ダイアグラムの作成では、分子の幾何構造をまず、例えば量子多体系の基底状態波動関数と基底状態エネルギーを近似するためのハートリー＝フォック法を用いて最適化しなければならない[2][20]。次に、上で決定された平衡構造からずれた一連の幾何構造 に対してエネルギーの一点計算を行う。エネルギーの一点計算は、分子中の原子の特定の配置に対する分子のポテンシャルエネルギー曲面の計算である。これらの計算の実行では、結合長は一定（平衡値）に保たれ、結合角のみがその平衡値から変化されなければならない。個々の幾何構造に対するエネルギーの一点計算は次に結合角に対してプロットされ、代表的なウォルシュ・ダイアグラムが生成される。

ウォルシュ・ダイアグラムの構造

編集
 
AH2分子（例えばH2O）に対するウォルシュ・ダイアグラム

AH2分子

編集

最も単純なAH2分子系に対して、ウォルシュは結合角を90° から180° に変化させる間の正準分子軌道に対するab initio軌道エネルギーをプロットすることによって最初の角度相関図を作成した。結合角がゆがんでいった時の、個々の軌道のエネルギーは図中の線に従い、これによって配座の関数として分子エネルギーを素早く近似できる。ウォルシュ縦座標が核反発を考慮しているか否かについては未だに不明であり、これについてはまだ論争が続いている[21]。水に対する典型的な予測結果は90° の結合角であり、これは実験から得られる104° には程遠い。せいぜい、この方法は曲がった分子と直線状の分子を区別できる程度である[2]。

この同じ概念は、水素化物ではないAB2およびBAC分子、HABおよびHAAH分子、四原子水素化物分子（AH3）、水素化物ではない四原子分子、H2AB分子、アセトアルデヒド、五原子分子（CH3I）、六原子分子（エチレン）、ベンゼンを含むその他の化学種にも適用できる。

反応性

編集

分子軌道理論と併用することで、ウォルシュ・ダイアグラムは反応性を予測する手段として用いることもできる。ウォルシュ・ダイアグラムを生成し、次に分子のHOMO/LUMOを決定することによって、分子がどれぐらい反応しやすいかを決めることができる。以下の例では、BH3およびCH3+といったAH3分子のルイス酸性が予測される。

6電子AH3分子は平面配座をとるべきである。平面型AH3のHOMO（1e’）は、結合の乱れにより、A-H結合が曲がって三角錐型を形成するにつれて不安定化する、と見ることができる。一つの原子中心に集中しているLUMOはよい電子受容体であり、BH3およびCH3+のルイス酸としての性質を説明する[22]。

ウォルシュの相関図は、関連する分子軌道エネルギー準位を予測するために使うこともできる。平面型CH3+から四面体型CH3-Nuへの水素原子の歪みは、C-Nu結合軌道（σ）の安定化を生じさせる[22]。

 
平面型AH3分子に対するウォルシュ・ダイアグラム
 
CH3+への求核付加に対する軌道相互作用図

その他の相関図

編集

その他の相関図には田辺・菅野ダイアグラムやオーゲル・ダイアグラム（英語版）がある。

脚注

編集
  1. ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). オンライン版:  (2006-) "Correlation diagram".
  2. ^ a b c Miller, C. S.; Ellison, M. (2015). “Walsh Diagrams: Molecular Orbital and Structure Computational Chemistry Exercise for Physical Chemistry”. J. Chem. Educ. 92 (6): 1040-1043. doi:10.1021/ed500813d. 
  3. ^ Chen, E.; Chang, T. (1998). “Walsh Diagram and the Linear Combination of Bond Orbital Method”. Journal of Molecular Structure: THEOCHEM 431: 127–136. doi:10.1016/S0166-1280(97)00432-6. 
  4. ^ Mulliken, R.S. (1955). “Structures of the Halogen Molecules and the Strength of Single Bonds”. J. Am. Chem. Soc. 77 (4): 884–887. doi:10.1021/ja01609a020. 
  5. ^ a b Walsh, A.D. (1953). “The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part I. AH2 Molecules”. J. Chem. Soc.: 2260–2266. doi:10.1039/JR9530002260. 
  6. ^ Walsh, A.D. (1953). “The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part II. AB2 and BAC Molecules”. J. Chem. Soc.: 2266–2288. doi:10.1039/JR9530002266. 
  7. ^ Walsh, A.D. (1953). “The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part III. HAB and HAAH Molecules”. J. Chem. Soc.: 2288–2296. doi:10.1039/JR9530002288. 
  8. ^ Walsh, A.D. (1953). “The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part IV. Tetratomic hydride molecules, AH3”. J. Chem. Soc.: 2296–2301. doi:10.1039/JR9530002296. 
  9. ^ Walsh, A.D. (1953). “The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part V. Tetratomic, non-hydride molecules, AB3”. J. Chem. Soc.: 2301–2306. doi:10.1039/JR9530002301. 
  10. ^ Walsh, A.D. (1953). “The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part VI. H2AB Molecules”. J. Chem. Soc.: 2306–2317. doi:10.1039/JR9530002306. 
  11. ^ Walsh, A.D. (1953). “The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part VII. A note on the near-ultra-violet spectrum of acetaldehyde”. J. Chem. Soc.: 2318–2320. doi:10.1039/JR9530002318. 
  12. ^ Walsh, A.D. (1953). “The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part VIII. Pentatomic molecules: CH3I Molecules”. J. Chem. Soc.: 2321–2324. doi:10.1039/JR9530002321. 
  13. ^ Walsh, A.D. (1953). “The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part IX. Hexatomic molecules: ethylene”. J. Chem. Soc.: 2325–2329. doi:10.1039/JR9530002325. 
  14. ^ Walsh, A.D. (1953). “The Electronic Orbitals, Shapes, and Spectra of Polyatomic Molecules. Part X. A note on the spectrum of benzene”. J. Chem. Soc.: 2330–2331. doi:10.1039/JR9530002330. 
  15. ^ Mulliken, R.S. (1955). “Bond Angles in Water-Type and Ammonia-Type Molecules and Their Derivatives”. J. Am. Chem. Soc. 77 (4): 887–891. doi:10.1021/ja01609a021. 
  16. ^ Walsh, A.D. (1976). “Some Notes on the Electronic Spectra of Small Polyatomic Molecules”. Int. Rev. Sci.: Phys. Chem., Ser. Two 3: 301–316. 
  17. ^ O'Leary, B.; Mallion, R.B. (1987). “Walsh Diagrams and the Hellman-Feynman Theorem: A Tribute to the Late Professor Charles A. Coulson, F.R.S. (1910-1974)”. Journal of Mathematical Chemistry 1 (4): 335–344. doi:10.1007/BF01205066. 
  18. ^ Atkins, P.W. (1970). Molecular Quantum Mechanics. Oxford, Massachusetts: Clarendon Press. ISBN 0-19-855129-0 
  19. ^ Peters, D. (1966). “Nature of the One-Electron Energies of the Independent Electron Molecular Orbital Theoryand the Walsh Diagrams”. [[Transactions of the Faraday Society|]] 6: 1353–1361. 
  20. ^ Chen, E.; Chang, T. (1997). “Orbital Interaction and the Mulliken-Walsh Diagram for AH2 Systems”. Journal of the Chinese Chemical Society (Taipei) 44: 559–565. 
  21. ^ Takahata, Y.; Parr, R.G. (1974). “Three Methods to Look at Walsh-type Diagrams Including Nuclear Repulsions”. Bulletin of the Chemical Society of Japan 47 (6): 1380–1386. doi:10.1246/bcsj.47.1380. 
  22. ^ a b Atkins, P.W.. (1970). Inorganic Chemistry: Shriver and Atkins. Oxford, U.K.: Oxford University Press. ISBN 978-0-19-926463-6 

関連項目

編集

外部リンク

編集
「https://ja.wiki.x.io/w/index.php?title=ウォルシュ・ダイアグラム&oldid=96463579」から取得